1. Friends, Romans, ...
Extend your ears to me for I will now discuss the Kan extension condition. An
important notion in topology is that of a “fibration”. Let us begin with two typical
examples.
Consider the unit circle S1 as the space parametrising lines through the origin. Let
M 
 2 × S1 be the “incidence locus” which consists of a point in
2 × S1 be the “incidence locus” which consists of a point in  2 and a line which
contains it; M is just another way of representing the Möbius strip. There is a natural
map M
2 and a line which
contains it; M is just another way of representing the Möbius strip. There is a natural
map M  S1. Any point on
S1. Any point on  2 other than the origin corresponds to a unique
point in M; moreover, any line L in
2 other than the origin corresponds to a unique
point in M; moreover, any line L in  2 that does not contain the origin maps
bijectively to S1 -{L0} where L0 is the line parallel to L through the origin.
Thus we see that M - L0 is isomorphic to the product of S1 -{L0} and a
line.
2 that does not contain the origin maps
bijectively to S1 -{L0} where L0 is the line parallel to L through the origin.
Thus we see that M - L0 is isomorphic to the product of S1 -{L0} and a
line.
Another example is the space Q of pairs of orthonormal vectors (v,w) (such that
v.v = w.w = 0 and v.w = 1) in  3. We have a natural map Q
3. We have a natural map Q  S2 sending (v,w) to v.
Given any fixed vector u, we can give a map from S2 -{u,-u} to Q by taking v to
(v,(v × u)/|v × u|). More generally, as u varies on a great circle S1 (i. e. the
intersection of S2 with a plane through the origin), we obtain a map S2 - S1 × S1 to
Q.
S2 sending (v,w) to v.
Given any fixed vector u, we can give a map from S2 -{u,-u} to Q by taking v to
(v,(v × u)/|v × u|). More generally, as u varies on a great circle S1 (i. e. the
intersection of S2 with a plane through the origin), we obtain a map S2 - S1 × S1 to
Q.
1.1. Fibrations. In each case we have a map f : X  Y such that each point y in Y
has a neighbourhood U such that f-1(U) is homeomorphic to U × f-1(y). Such a
map has traditionally been called a “fibre bundle”. However, the required of
“locally product-like” is too restrictive since we are only studying spaces “upto
homotopy”.
From a topological point of view the important property of such a map is “path
lifting” or more generally “homotopy extension”. Given any “test” space T and a
closed subspace S, and a homotopy F : T × I
Y such that each point y in Y
has a neighbourhood U such that f-1(U) is homeomorphic to U × f-1(y). Such a
map has traditionally been called a “fibre bundle”. However, the required of
“locally product-like” is too restrictive since we are only studying spaces “upto
homotopy”.
From a topological point of view the important property of such a map is “path
lifting” or more generally “homotopy extension”. Given any “test” space T and a
closed subspace S, and a homotopy F : T × I  Y , such that F0 : T
Y , such that F0 : T  Y
“lifts” to G0 : T
Y
“lifts” to G0 : T  X, and the homotopy itself can be lifted along S, this lift
can be extended to G : T × I
X, and the homotopy itself can be lifted along S, this lift
can be extended to G : T × I  Y . In other words, if we have a commutative
diagram
Y . In other words, if we have a commutative
diagram
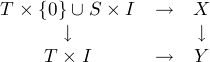
where the left vertical arrow is the subspace inclusion, then there is a lift T ×I  X. A
map X
X. A
map X  Y of this kind has traditionally been called a “fibration” in algebraic
topology.
Y of this kind has traditionally been called a “fibration” in algebraic
topology.
Replacing topological spaces everywhere with simplicial complexes and the interval I
with  [1] we come up with the following notion of fibration of simplicial complexes. A
map X
[1] we come up with the following notion of fibration of simplicial complexes. A
map X  Y of simplicial complexes is called a “fibration” if for any a complex K and
any subcomplex L of K, and any diagram
Y of simplicial complexes is called a “fibration” if for any a complex K and
any subcomplex L of K, and any diagram
![K × {e}U L × D[1] --> X
|, |,
K × D[1] --> Y](kan1x.png)
we have a map K ×  [1]
[1]  X that “completes” the diagram as above. Here e is either
of the two vertices of
X that “completes” the diagram as above. Here e is either
of the two vertices of  [1]. A further technical requirement in this case is that X0
[1]. A further technical requirement in this case is that X0  Y 0
must be surjective.
Y 0
must be surjective.
1.2. Reduction to basic cases. The above condition needs to checked for all
complexes K and all sub-complexes L; this seems to be too much. Can we reduce this to
a simpler condition?
Suppose that  is the smallest simplex of K that is not in L. Then the faces
of
is the smallest simplex of K that is not in L. Then the faces
of  lie in L so, using the map
lie in L so, using the map  [n]
[n]  K given by
K given by  , we get a commutative
diagram
, we get a commutative
diagram
![D[n]× {e}U @D[n] ×D[1] --> K × {e} U L× D[1]
|, |,
D[n]× D[1] --> K × D[1]](kan2x.png)
Combining this with the above, we get a diagram
![D[n] × {e}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan3x.png)
If can complete this diagram with a map  [n] ×
[n] ×  [1]
[1]  X, we can “add”
X, we can “add”  to L and
repeat the process. Now the last diagram is a particular case of the fibration diagram
with K =
to L and
repeat the process. Now the last diagram is a particular case of the fibration diagram
with K =  [n] and L =
[n] and L = 
 [n]. Thus we see that an equivalent formulation of the
fibration requirement is the completion of the last diagram and the surjectivity of
X0
[n]. Thus we see that an equivalent formulation of the
fibration requirement is the completion of the last diagram and the surjectivity of
X0  Y 0.
Y 0.
1.3. Even simpler. The subcomplex  [n] ×{e}
[n] ×{e}
 [n] ×
[n] ×  [1] of the simplicial
complex
[1] of the simplicial
complex  [n] ×
[n] ×  [n] can be thought of as the boundary of a cylinder with one side
capped contained in the solid cylinder. Another figure that is topologically similar is the
inclusion of the boundary of a simplex with one face removed into the full simplex. Let
[n] can be thought of as the boundary of a cylinder with one side
capped contained in the solid cylinder. Another figure that is topologically similar is the
inclusion of the boundary of a simplex with one face removed into the full simplex. Let
 k[N] denote the subcomplex of
k[N] denote the subcomplex of 
 [n] in which the k-th face has been removed.
The homotopy extension condition can be written as a lifting condition for the
diagram:
[n] in which the k-th face has been removed.
The homotopy extension condition can be written as a lifting condition for the
diagram:
![/\k[n] --> X
|, |,
D[n] --> Y](kan4x.png)
Let X  Y be a morphism of simplicial complexes. We say that it satisfies the Kan
extension condition if for every such diagram we have a lifting
Y be a morphism of simplicial complexes. We say that it satisfies the Kan
extension condition if for every such diagram we have a lifting  [n]
[n]  X which
completes the diagram.
X which
completes the diagram.
1.4. Equivalence. Let X  Y be a morphism that satisfies the Kan extension
condition. First of all note that
Y be a morphism that satisfies the Kan extension
condition. First of all note that 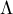 0[0] is the empty simplicial complex. Thus the Kan
extension condition for n = 0 translates into the surjectivity of the map X0
0[0] is the empty simplicial complex. Thus the Kan
extension condition for n = 0 translates into the surjectivity of the map X0  Y 0. We
wish to show that X
Y 0. We
wish to show that X  Y is a fibration. By showing that a diagram of the
form
Y is a fibration. By showing that a diagram of the
form
![D[n] × {e}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan5x.png)
We first note that  [n] ×
[n] ×  [1] is the simplicial complex associated with the partially
ordered set [0,n] × [0,1] where (i,j) < (k,l) if i < k and j < l. A non-degenerate
k-simplex of this complex is associated with a strictly increasing sequence of k + 1
elements from this partially-ordered set. In particular, there are n + 1 n + 1-simplices,
each is associated with a sequence like (0,0) <
[1] is the simplicial complex associated with the partially
ordered set [0,n] × [0,1] where (i,j) < (k,l) if i < k and j < l. A non-degenerate
k-simplex of this complex is associated with a strictly increasing sequence of k + 1
elements from this partially-ordered set. In particular, there are n + 1 n + 1-simplices,
each is associated with a sequence like (0,0) <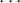 < (i,0) < (i,1) <
< (i,0) < (i,1) <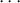 < (n,1); we
denote this simplex by
< (n,1); we
denote this simplex by  i. Similarly, an n-simplex that lies in
i. Similarly, an n-simplex that lies in 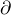
 [n] ×
[n] ×  [1] is associated
with a sequence of the type
[1] is associated
with a sequence of the type
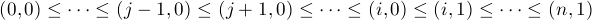
or
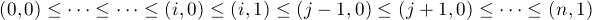
Thus the two faces of  i that are not in
i that are not in 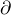
 [n] ×
[n] ×  [1] are associated
with the sequences (0,0) <
[1] are associated
with the sequences (0,0) < < (i - 1,0) < (i,1) <
< (i - 1,0) < (i,1) <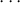 < (n,1) and
(0,0) <
< (n,1) and
(0,0) <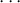 < (i,0) < (i + 1,1) <
< (i,0) < (i + 1,1) <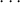 < (n,1). Depending on whether e is 0 or 1 the face
dn+1
< (n,1). Depending on whether e is 0 or 1 the face
dn+1 n, or d0
n, or d0 0 respectively, is
0 respectively, is  [n] ×{e,}. Let us assume that e is 0 as we can argue in
a simlar fashion in the other case. The map
[n] ×{e,}. Let us assume that e is 0 as we can argue in
a simlar fashion in the other case. The map ![D[n]× {0} U @D[n]× D[1]-- > X](kan14x.png) is already
defined on all faces of
is already
defined on all faces of  n except dn
n except dn n. Thus we obtain a map
n. Thus we obtain a map 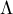 n[n + 1]
n[n + 1]  X which lifts
the map
X which lifts
the map  [n + 1]
[n + 1]  Y that corresponds to the image of
Y that corresponds to the image of  n in Y . By the Kan extension
condition, we obtain a lifting
n in Y . By the Kan extension
condition, we obtain a lifting  [n + 1]
[n + 1]  X of
X of  n; in particular, we also obtain a lift of
dn
n; in particular, we also obtain a lift of
dn n. This latter is also dn
n. This latter is also dn n-1. Thus, we obtain a lift of the map given by
n-1. Thus, we obtain a lift of the map given by  n-1 to all
its faces except dn-1
n-1 to all
its faces except dn-1 n-1. This gives a map
n-1. This gives a map 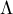 n-1[n + 1]
n-1[n + 1]  X to which we again apply
the Kan extension condition. Using the fact that di
X to which we again apply
the Kan extension condition. Using the fact that di i-1 = di
i-1 = di i, we can proceed by
induction to lift each of the simplices
i, we can proceed by
induction to lift each of the simplices  i to X; hence we have the homotopy extension as
required.
i to X; hence we have the homotopy extension as
required.
To prove the converse, we note that if X  Y is a simplicial fibration then X0
Y is a simplicial fibration then X0  Y 0
is a surjection by assumption. Thus we only need to prove the Kan extenion condition for
simplices of dimension n + 1 where n > 0.
Y 0
is a surjection by assumption. Thus we only need to prove the Kan extenion condition for
simplices of dimension n + 1 where n > 0.
For each integer k between 0 and n there is an order preserving surjective map
fk : [0,n] × [0,1]  [0,n + 1]
[0,n + 1]
Such an order preserving map induces a map of simplicial complexes  [n] ×
[n] ×  [1]
[1] 
 [n + 1]
that we will denote by the same letter by abuse of notation. If
[n + 1]
that we will denote by the same letter by abuse of notation. If  is a strictly increasing
sequence on [0,n] × [0,1] which contains at least one pair (t,0) and (t,1) for t
is a strictly increasing
sequence on [0,n] × [0,1] which contains at least one pair (t,0) and (t,1) for t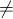 k then
the image of this sequence under fk is not strictly increasing; in other words, the image
of the corresponding non-degenerate simplex is degenerate. In particular, the image of
the n + 1-simplex
k then
the image of this sequence under fk is not strictly increasing; in other words, the image
of the corresponding non-degenerate simplex is degenerate. In particular, the image of
the n + 1-simplex  l is non-degenerate only if l = k; the image of
l is non-degenerate only if l = k; the image of  k is the
non-degenerate n + 1-simplex in
k is the
non-degenerate n + 1-simplex in  [n + 1]. Similarly, the image of an n-simplex that is
contained in di
[n + 1]. Similarly, the image of an n-simplex that is
contained in di [n] ×
[n] ×  [1] is non-degenerate only if it is di
[1] is non-degenerate only if it is di k for i < k and di+1
k for i < k and di+1 k
for i > k; the image of this n-simplex is the corresponding face of
k
for i > k; the image of this n-simplex is the corresponding face of  [n + 1].
Finally, the faces dk
[n + 1].
Finally, the faces dk k and dk+1
k and dk+1 k are the images of
k are the images of  [n] ×{1} and
[n] ×{1} and  [n] ×{0}
respectively.
[n] ×{0}
respectively.
To summarise, we have obtain a simplicial map fk :  [n] ×
[n] ×  [1]
[1] 
 [n + 1] which
maps the
[n + 1] which
maps the 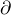
 [n] ×
[n] ×  [1]
[1] 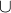
 [n] ×{0} to
[n] ×{0} to  k[n + 1] and maps
k[n + 1] and maps 
 [n] ×
[n] ×  [1]
[1] 
 [n] ×{1} to
[n] ×{1} to
 k+1[n + 1]. Moreover, the only n + 1-simplex whose image is non-degenerate is
k+1[n + 1]. Moreover, the only n + 1-simplex whose image is non-degenerate is  k.
Given a diagram
k.
Given a diagram
![/\ [n + 1] --> X
k |, |,
D[n+ 1] --> Y](kan17x.png)
we obtain a diagram
![D[n] ×{0}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan18x.png)
If the map X  Y has the homotopy extension property we obtain a map
Y has the homotopy extension property we obtain a map
 [n] ×
[n] ×  [1]
[1]  X. Restricting this to
X. Restricting this to  k we obtain the required lifting
k we obtain the required lifting  [n + 1]
[n + 1]  X. We
can argue similarly with
X. We
can argue similarly with  k+1[n + 1]. We conclude that the Kan extension propery
follows from the homotopy extension property as well.
k+1[n + 1]. We conclude that the Kan extension propery
follows from the homotopy extension property as well.
Assignment.
- Let F be a set and define a simplicial complex K by setting Kn = F and
all maps to be identity. Show that this is a simplicial complex. We denote
this simplicial complex by the same symbol F and call it the “constant” or
discrete complex. Show that it is a Kan complex.
- Let F be a set and define a simplicial complex K = E(F) by setting
Kn = Fn+1 (F ×
 × F taken n times). Define the boundary map
di : Fn+1
× F taken n times). Define the boundary map
di : Fn+1  Fn as the map that “forgets” the i-th entry in the n+1-tuple.
Define si : Fn
Fn as the map that “forgets” the i-th entry in the n+1-tuple.
Define si : Fn  Fn+1 as the map that duplicates the i-the entry. Show
that this is a simplicial complex. Is it a Kan complex?
Fn+1 as the map that duplicates the i-the entry. Show
that this is a simplicial complex. Is it a Kan complex?
 2 × S1 be the “incidence locus” which consists of a point in
2 × S1 be the “incidence locus” which consists of a point in  2 and a line which
contains it; M is just another way of representing the Möbius strip. There is a natural
map M
2 and a line which
contains it; M is just another way of representing the Möbius strip. There is a natural
map M  S1. Any point on
S1. Any point on  2 other than the origin corresponds to a unique
point in M; moreover, any line L in
2 other than the origin corresponds to a unique
point in M; moreover, any line L in  2 that does not contain the origin maps
bijectively to S1 -{L0} where L0 is the line parallel to L through the origin.
Thus we see that M - L0 is isomorphic to the product of S1 -{L0} and a
line.
2 that does not contain the origin maps
bijectively to S1 -{L0} where L0 is the line parallel to L through the origin.
Thus we see that M - L0 is isomorphic to the product of S1 -{L0} and a
line.
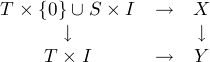
 [1] we come up with the following notion of fibration of simplicial complexes. A
map
[1] we come up with the following notion of fibration of simplicial complexes. A
map ![K × {e}U L × D[1] --> X
|, |,
K × D[1] --> Y](kan1x.png)

![D[n]× {e}U @D[n] ×D[1] --> K × {e} U L× D[1]
|, |,
D[n]× D[1] --> K × D[1]](kan2x.png)
![D[n] × {e}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan3x.png)
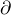
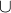
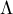
![/\k[n] --> X
|, |,
D[n] --> Y](kan4x.png)
![D[n] × {e}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan5x.png)
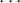
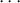
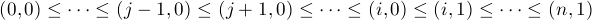
![D[n]× {0} U @D[n]× D[1]-- > X](kan14x.png) is already
defined on all faces of
is already
defined on all faces of 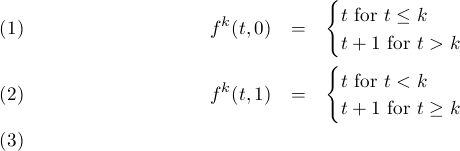
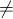
![/\ [n + 1] --> X
k |, |,
D[n+ 1] --> Y](kan17x.png)
![D[n] ×{0}U @D[n] × D[1] --> X
|, |,
D[n] × D[1] --> Y](kan18x.png)