AN INTRODUCTION TO ALGEBRAIC TOPOLOGY
KAPIL HARI PARANJAPE
Introduction
There are three different ways in which mathematicians have reached the subject now
called algebraic topology:
- Classification, properties and invariants. One looks for ways of
distinguishing topological spaces.
- Obstructions. What are the difficulties in getting certain types of maps
between spaces.
- Categorical. What is the structure of the category of topological spaces or
some subcategories of it?
As one realises during the study of algebraic topology all these are different ways of
stating the same question--and the answer is to apply the methods of algebraic
topology.
Classification. The method of “divide and conquer” can be applied to break the study
of “all” topological spaces into a number of different classes. For example we can see
that the real line  is not homeomorphic to
is not homeomorphic to  -{0} because the former is
connected while the latter is not. Similarly, the real line
-{0} because the former is
connected while the latter is not. Similarly, the real line  is not homeomorphic
to the circle S1 = {(x,y)|x2 + y1 = 1}, which is a subspace of
is not homeomorphic
to the circle S1 = {(x,y)|x2 + y1 = 1}, which is a subspace of  2, because
the latter is compact but the former is not. One way of stating the goal of
algebraic topology is to say that we want to find enough such properties to
classify all spaces upto homeomorphism. However, this proves too hard and
we must restrict ourselves to some class of “reasonable” spaces (as shown by
Steenrod one such class is the collection of “compactly-generated spaces”);
further, we must weaken the equivalence of spaces to “homotopy equivalence”
instead of homeomorphism. Even this problem is too hard based on “computable”
invariants and so the problem is usually reduced to the study of “weak homotopy
equivalence” of these spaces or the study of a still smaller class of spaces called
CW-complexes.
2, because
the latter is compact but the former is not. One way of stating the goal of
algebraic topology is to say that we want to find enough such properties to
classify all spaces upto homeomorphism. However, this proves too hard and
we must restrict ourselves to some class of “reasonable” spaces (as shown by
Steenrod one such class is the collection of “compactly-generated spaces”);
further, we must weaken the equivalence of spaces to “homotopy equivalence”
instead of homeomorphism. Even this problem is too hard based on “computable”
invariants and so the problem is usually reduced to the study of “weak homotopy
equivalence” of these spaces or the study of a still smaller class of spaces called
CW-complexes.
Obstructions. A different way of approaching the problem is through the study of
continuous maps. Instead of asking whether  is homeomorphic to S1 we can
ask whether the map t
is homeomorphic to S1 we can
ask whether the map t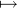 (cos(t),sin(t)) has an inverse. Such questions arise
naturally in other contexts also. For example, to each line in the plane we can
associate an angle. Can we find a parametric family of lines which is (continuously)
parametrised by the angle of the line? Can we find such a parametric family that is
at unit distance from the origin? As another example consider equations of
the form x3 + ax + b = 0 with a and b real; we know that such an equation
always has a solution. Can we find a (continuous) function f(a,b) that gives a
solution?
The study of such problems is called obstruction theory. It too leads to algebraic
topology in a natural way. For example, we can show that there is no surjective contiuous
map from
(cos(t),sin(t)) has an inverse. Such questions arise
naturally in other contexts also. For example, to each line in the plane we can
associate an angle. Can we find a parametric family of lines which is (continuously)
parametrised by the angle of the line? Can we find such a parametric family that is
at unit distance from the origin? As another example consider equations of
the form x3 + ax + b = 0 with a and b real; we know that such an equation
always has a solution. Can we find a (continuous) function f(a,b) that gives a
solution?
The study of such problems is called obstruction theory. It too leads to algebraic
topology in a natural way. For example, we can show that there is no surjective contiuous
map from  to
to  -{0} because the latter is disconnected. Similarly, there is no
surjective continuous map from S1 to
-{0} because the latter is disconnected. Similarly, there is no
surjective continuous map from S1 to  since the former is compact. Thus the invariants
of algebraic topology can be used to solve problems in obstruction theory as well. In fact,
and perhaps surprisingly, the problem of classification can be reduced to problems in
obstruction theory.
since the former is compact. Thus the invariants
of algebraic topology can be used to solve problems in obstruction theory as well. In fact,
and perhaps surprisingly, the problem of classification can be reduced to problems in
obstruction theory.
Category Theory. The relation between classification and obstruction can be better
understood if we look at the totality (carefully avoiding Russellian paradoxes)
of spaces and maps. The algebraic mechanism for this is called a category. A
category is defined by its objects and morphisms. Morphisms can be composed and
composition is associative. For each object we have an identity morphism from
the object to itself which acts as a both sided identity for composition. As an
important example, we can take the category of topological spaces; its objects are
topological spaces and morphisms are continuous maps between topological
spaces.
The problem of classification can thus be re-stated as the study of this category; can
one find an algebraic description of this category that does not refer to the underlying
notions of topological spaces and continuous maps. As an example of such a description
consider the category of all vector spaces over a field (say  ), with morphisms given by
linear maps. The theorem of basis for vector spaces and the matrix representation of
morphisms says that this category can be “represented” as the category whose
objects are non-negative integers and morphisms between n and m are n × m
matrices.
), with morphisms given by
linear maps. The theorem of basis for vector spaces and the matrix representation of
morphisms says that this category can be “represented” as the category whose
objects are non-negative integers and morphisms between n and m are n × m
matrices.
Different approaches. There are essentially three approaches to the study of algebraic
topology corresponding to the three categories that arise there. First of all there is the
Steenrod category of compactly generated spaces. Next there is Whitehead’s category of
CW-complexes and finally there is Kan’s category of simplicial complexes; this list in
increasing order of “algebraic”-ness. Ultimately, the result is going to say that Kan’s
category will capture all the computable algebraic topological invariants of the other two
categories. In the interest of “concrete”-ness it seems (to me!) to be better to start
with this category as it restricts the types of spaces that we will study and the
kinds of maps allowed between them. Thus the study will be much simpler than
the study of “all” topological spaces and “all” continuous maps; as we shall
see we can (essentially) construct these spaces out of building blocks as also
construct maps out of simple incidence and collapsing maps. Of course, the
problem of studying more general spaces and more general maps will remain. This
will be resolved by proving triangulability and the simplicial approximation
theorem.
A final word of advice. Since are taking a very algebraic approach it is possible that
what we will do will look “abstract”. The solution is to think geometrically and write
algebraically. It is easier to verify (line by line) a well-written algebraic computation but
it is easier to contruct/re-construct one if we can visualise the geometric meaning of each
step.
Assignment.
- Classify the letters of any alphabet (of your choice) upto homeomorphism.
Can you prove the above classification? Between which classes are their
injective or surjective continuous maps?
- Give a topological classification of plane conics. Prove this classification.
- Let S3 be the 3-sphere (unit vectors in 4-space). Show that it is possible to
choose a continuous map f : S3
 S3 such that f(v) is orthogonal to v. Is
this possible for S2? What about S1?
S3 such that f(v) is orthogonal to v. Is
this possible for S2? What about S1?
- Let P be the category whose objects are polynomials f(x) over a field k. A
morphism h : f
 g is a polynomial h(x) such that g(h(x)) = f(x). Relate
this category to some subcategory of the category of rings.
g is a polynomial h(x) such that g(h(x)) = f(x). Relate
this category to some subcategory of the category of rings.
 is not homeomorphic to
is not homeomorphic to  -{0} because the former is
connected while the latter is not. Similarly, the real line
-{0} because the former is
connected while the latter is not. Similarly, the real line  is not homeomorphic
to the circle S1 = {(x,y)|x2 + y1 = 1}, which is a subspace of
is not homeomorphic
to the circle S1 = {(x,y)|x2 + y1 = 1}, which is a subspace of  2, because
the latter is compact but the former is not. One way of stating the goal of
algebraic topology is to say that we want to find enough such properties to
classify all spaces upto homeomorphism. However, this proves too hard and
we must restrict ourselves to some class of “reasonable” spaces (as shown by
Steenrod one such class is the collection of “compactly-generated spaces”);
further, we must weaken the equivalence of spaces to “homotopy equivalence”
instead of homeomorphism. Even this problem is too hard based on “computable”
invariants and so the problem is usually reduced to the study of “weak homotopy
equivalence” of these spaces or the study of a still smaller class of spaces called
CW-complexes.
2, because
the latter is compact but the former is not. One way of stating the goal of
algebraic topology is to say that we want to find enough such properties to
classify all spaces upto homeomorphism. However, this proves too hard and
we must restrict ourselves to some class of “reasonable” spaces (as shown by
Steenrod one such class is the collection of “compactly-generated spaces”);
further, we must weaken the equivalence of spaces to “homotopy equivalence”
instead of homeomorphism. Even this problem is too hard based on “computable”
invariants and so the problem is usually reduced to the study of “weak homotopy
equivalence” of these spaces or the study of a still smaller class of spaces called
CW-complexes.
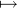 (cos(
(cos(