


Next: Polynomials and polynomial functions
Up: Pre-requisites
Previous: Introduction of co-ordinates
In the co-ordinate plane one can study more general geometric figures
that those desribed by lines. In this section we undertake a rigorous
study of conic sections. In particular, we find geometric criteria
that distinguish the different conics. We also establish Steiner's
construction of conic sections as the locus of intersection of a pair
of rotating lines.
The first equation that is more complicated that the equation of a
line as given above is one of the form
ax2 + bxy + cy2 + dx + ey + f = 0
where a, b and c are not all zero (in which case the equation
would become that of a line). The locus of points (x, y) that
satisfy this equation is called a conic or a conic section.
Figure 4:
The Smooth Conics
|
|
By plotting the corresponding curves we find that we have the
following types of conics:
- There are no solutions.
- The solutions all lie on one line.
- The solutions all lie on a pair of lines.
- The conic lies within a bounded region of the plane
(i. e. the conic is compact). This called an ellipse (of which the
circle is a special case).
- The conic has two parts (i. e. the conic is disconnected).This
is called a hyperbola.
- The conic is connected and not compact. This is called a
parabola.
We note that the first three types are distinguished without reference
to order among numbers (or separation axioms in geometry) and so make
sense over other fields. We will see below how we can distinguish the
other conics in a purely algebraic way.
Exercise 5
Find ways of distinguishing the different conics by looking at the
equation. (Hint: Examine the discriminant b2 - 4ac).
For any line ax + by + c = 0 with a non-zero, we can write the solutions
in terms of one parameter as
(-bt-c/a, t); similarly when b
is not zero. We can also ``solve'' a conic. Let us suppose that the
conic is not of type (1), (2) or (3) above. Fix a point (x0, y0) on
the conic.
Exercise 6
We will find a parametric solution of a conic. (Hint: Use
translation and scaling of co-ordinates to simplify the equations
wherever possible).
- Let
(y - y0) = t(x - x0) be a line through this point. Show that
there is at most one other point of the conic that lines on this
line.
- Find the co-ordinates of this point in terms of the constants
a, b, c, d, e, f, x0, y0 and the parameter t.
- Show that this parametric solution is not well defined at two
values of t for a hyperbola.
- Show that this parametric solution misses one point in the
case of an ellipse or circle but is well-defined at all values of
t.
- Show that this parametric solution is not well defined for one
value of t and misses one point or is well defined and misses no
points on a parabola.
This can be carried further through Steiner's construction as follows.
Let (x1, y1) another point on the conic.
Exercise 7
Show that there are constants
A,
B,
C and
D so that for any
point (
x2,
y2) of the conic we have
Moreover, these constants are such that if we try to solve for
s =
t, we obtain no solutions when the conic is an ellipse (or
circle), one solution for a parabola and two solutions for a
hyperbola.
Figure 5:
Steiner's Construction
|
|
The geometric content of this is the statement that the conic is
obtained as the locus of intersection of a pair of rotating lines
based at (x0, y0) and (x1, y1) respectively with respective
slopes s and t related by
s(Ct + D) = At + D.
Exercise 8
Prove the converse that such a locus is always a conic.



Next: Polynomials and polynomial functions
Up: Pre-requisites
Previous: Introduction of co-ordinates
Kapil H. Paranjape
2001-01-20

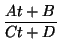 whent =
whent =