


Next: 7.1 Prime ideals
Up: Some Lectures on Number
Previous: 6.7 Prime ideals
We now specialise the results of the previous section to the case of
extensions of
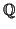 of degree 2. Such a field is of the form
of degree 2. Such a field is of the form
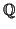 [T]/P(T) where P(T) is an irreducible polynomial of degree 2.
An order in such a field is generated by 1 and a non-rational element
[T]/P(T) where P(T) is an irreducible polynomial of degree 2.
An order in such a field is generated by 1 and a non-rational element
 that satisfies an equation of the type
P(T) = T2 - bT + c. Thus
every order has the form R[T]/P(T). Now, it is clear that
Trace(
that satisfies an equation of the type
P(T) = T2 - bT + c. Thus
every order has the form R[T]/P(T). Now, it is clear that
Trace( ) = b and
Nm(
) = b and
Nm( ) = c. Moreover,
Trace(
) = c. Moreover,
Trace(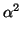 ) = Trace(b
) = Trace(b - c) = b2 - 2c. Thus the discriminant
DR of R is the determinant of
- c) = b2 - 2c. Thus the discriminant
DR of R is the determinant of
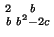
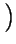 which is b2 - 4c (as expected). In particular, we see that
DR = b2(mod 4); i. e. the discriminant must be 0 or 1 modulo 4. In
the first case, we can replace
which is b2 - 4c (as expected). In particular, we see that
DR = b2(mod 4); i. e. the discriminant must be 0 or 1 modulo 4. In
the first case, we can replace  by
by
 + (b - 1)/2 so that we
get an element with trace 1. In the second case, we can replace
+ (b - 1)/2 so that we
get an element with trace 1. In the second case, we can replace
 by
by
 + b/2 to get an element with trace 0. Thus we can
assume that the equation takes the form T2 - T + N in the first case
and T2 + N in the second case. An alternative normalisation is to
replace
+ b/2 to get an element with trace 0. Thus we can
assume that the equation takes the form T2 - T + N in the first case
and T2 + N in the second case. An alternative normalisation is to
replace  by
by
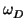 = (DR +
= (DR + 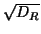 )/2 in both cases; this
can be done since DR + b is even in both cases. We thus have a
natural basis for R. There is also a natural involution on R which
sends
)/2 in both cases; this
can be done since DR + b is even in both cases. We thus have a
natural basis for R. There is also a natural involution on R which
sends
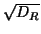 to
-
to
- 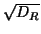 or equivalently
or equivalently 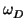 to
DR -
to
DR - 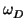 .
.
Subsections



Next: 7.1 Prime ideals
Up: Some Lectures on Number
Previous: 6.7 Prime ideals
Kapil Hari Paranjape
2002-10-20