Mott transition physics
Despite the Bloch's band theory and the contemporary density functional theory (DFT) being successful in explaining why some materials behave like semiconductors or insulators, many contradicting behaviors have been observed experimentally in many solid state materials which demands a new theory. Particularly in 1937, de Boer and Verwey reported transparent insulating behavior of transition metal oxides like NiO and CoO even though their incomplete d-shells predict them to be metals from the band theory perspective. Nevil Mott argued that the Coulomb repulsion between electrons prevents the electrons to conduct and hence such materials are coined as the Mott insulators.

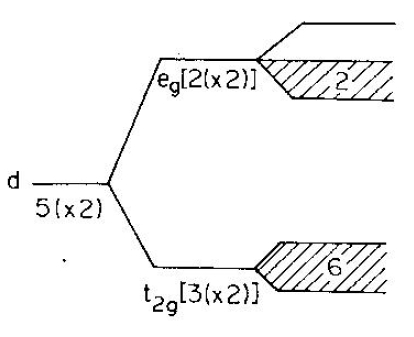
Several transition metal oxides (including the famous cuprate superconductors) and organic materials show transition from metal to Mott insulator transition under change in pressure, chemical doping, or temperature. The metallic phase of such materials often show high resistivity and specific heat coefficient and hence in that phase they are termed 'bad metals'. Nevertheless bad metals can be explained in terms of renormalized or dressed free electrons, called the quasiparticle, due to the presence of Coulomb interactions. This renormalized free electron theory is known as the Fermi liquid theory. Our main interest is to investigate what happens to such Fermi liquid electrons in a lattice when the Coulomb interaction is turned on. A minimalistic model Hamiltonian that captures such physics is the Hubbard model. In the second quantization form the model is formally written as
$\hat H_{\text{Hubbard}}=-t\sum_{\langle ij\rangle,\sigma}[c^{\dagger}_{i\sigma}c_{j\sigma} + c^{\dagger}_{j\sigma}c_{i\sigma}] -\mu\sum_{i,\sigma}\hat n_{i\sigma} +U\sum_i \hat n_{i\uparrow} \hat n_{i\downarrow}$
where $t$ is amplitude of nearest-neighbor hopping (overlap of atomic orbitals) site $i$ to site $j$, $\mu$ is the chemical potential and operator $c^{\dagger}_{i\sigma}$ and $c_{j\sigma}$ creates and destroys an electron with spin $\sigma$ at site $i$ respectively ($\hat n_{i\sigma}=c^{\dagger}_{i\sigma}c_{i\sigma}$), and $U$ is the local Coulomb repulsion. Hubbard model is not solvable analytically except in one dimension. Therefore several numerical methods have developed during the '90s and one such method is the dynamical mean-field theory (DMFT) which gained immense popularity in the scientific community as it successfully captures the MIT due to the Coulomb interaction present in the Hubbard model. I am interested in exploiting the potentiality of DMFT for the Hubbard and other correlated lattice models.
Issues addressed :In general the Hubbard model could be solved exactly at two limits : $U=0$ (non-interacting limit) and $t=0$ (atomic limit). $U=0$ limit gives rise to a metallic phase with a tight-binding dispersion and $t=0$ limit shows up insulating phase with localized atomic orbitals. In this sense one hopes to get an interpolation between metallic and insulating phases when both $t$ and $U$ are finite. Unfortunately standard mean-field theories can capture only metallic or insulating phase. We employed the DMFT method for the Hubbard model and developed an improved version of the quantum improved solver (described in next section) IPT to seek finite temperature ($T$) properties. We find the following phase diagram on $T$-$U$ plane showing both interaction and temperature driven metal-to-insulator transition in presence of hysteresis, i.e. transition lines are different while $U$ is increased or decreased starting from a metallic or insulating phase respectively.
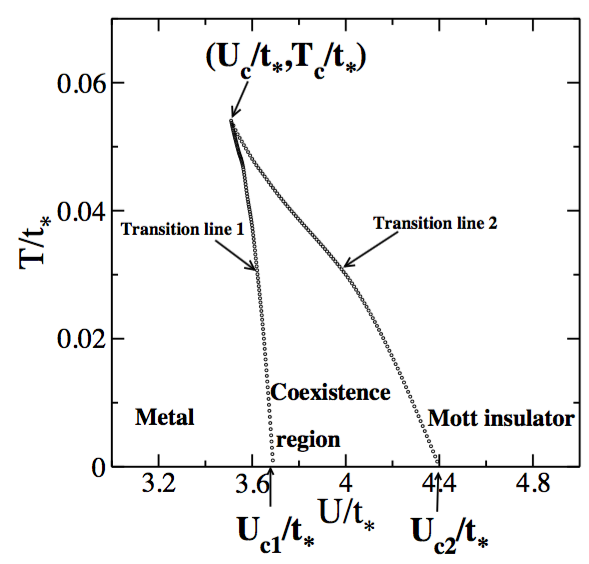
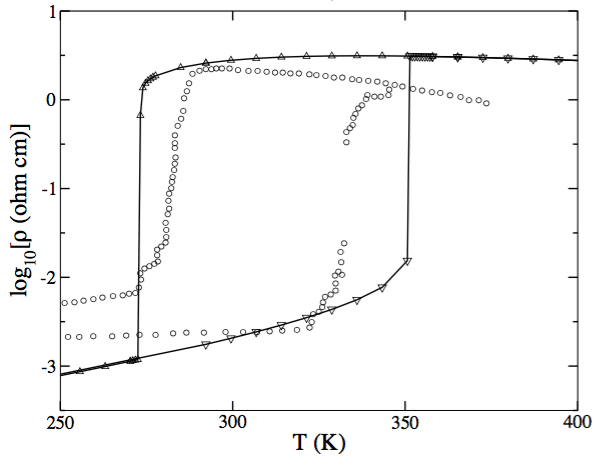
Such a hysteresis reflects on the transport property such as resistivity and we compare our result with resistivity found in experiment on vanadium sesquoxide (V$_2$O$_3$) and our best fit yields $U=3.6t_*$ with $t_*\simeq 0.63$ eV.
The work has been published at Int. J. Mod. Phys. B 25 2461-2479 (2011), A free version is available at arxiv.org : http://arxiv.org/abs/1011.4478
Quantum impurity solvers
Within the DMFT an interacting lattice model is envisaged as an effective quantum impurity model connected self-consistently to a non-interacting reservoir. Though such mapping to an effective impurity model simplifies the original lattice problem, quantum impurity model itself has remained a challenge dating back to the famous Kondo problem during '70s. This problem has become more intriguing in recent experiments with quantum dots in mesoscopic devices. In the context of DMFT, several numerical approaches have been formulated to address the impurity problem and those approaches are often dubbed quantum impurity solvers (QIS), to name a few, numerical renormalization group (NRG), iterated perturbation theory (IPT), Non-crossing approximation (NCA), exact diagonalization (ED), density matrix renormalization group (DMRG), Hirsh-Fye and continuous time quantum Monte Carlo (HFQMC and CTQMC). Despite such a large number of existing QISs, only IPT and NCA are semianalytical (i.e. Green's functions or self-energies can be obtained through analytical expressions) and hence less computationally expensive. Semianalyticity also promises to gain quick insights for an extended version of the lattice problem (such as one involving multiple orbitals, spin-orbit or electron-phonon coupling). Therefore finding a computationally faster and reliable QIS in demand.
Issues addressed :
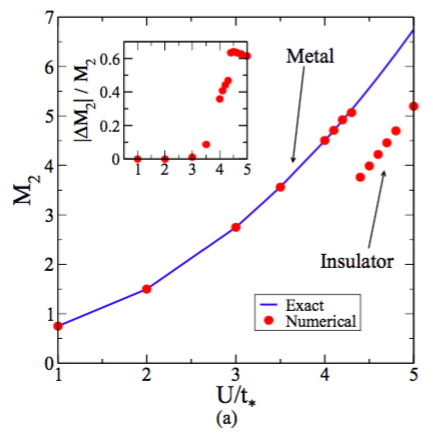
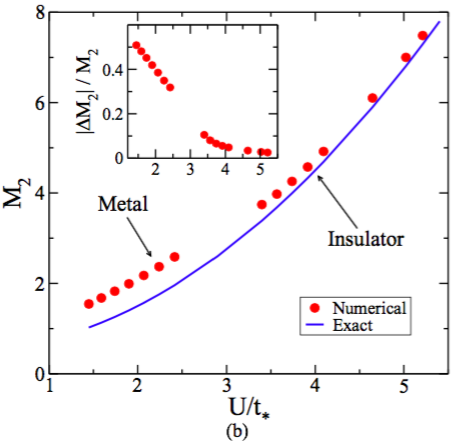
Instead of following the most popular ones, we investigated the single band Hubbard model at arbitrary filling within DMFT using local moment approach (LMA) as the QIS. Like IPT and NCA, LMA is also a semianalytical QIS and was originally pioneered by David Logan and his co-workers. LMA incorporates spin-dependent self-energies constructed up on all transverse spin-flip scattering polarization propagators through an RPA sum (this is equivalent to GW self-energy used in modern DFT-based problems). This additional spin-flip physics lets LMA become significantly different and better QIS compared to other semianalytical ones such as IPT. For instance, the second moment ($M_2$) of density of states (DoS) becomes more accurate at large $U$ in LMA whereas it breaks down severely in the insulating regime in IPT (See figure below).
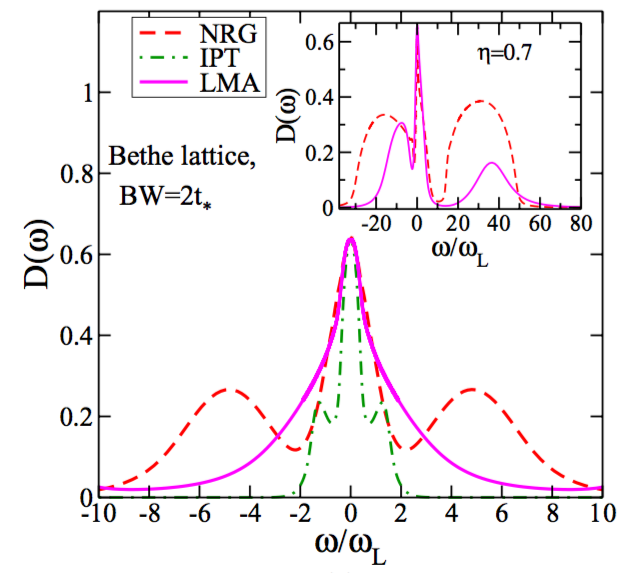
When we scale interacting DoS by the low energy Fermi liquid scale ($\omega_L=Zt_*$, $Z$ is quasiparticle residue), LMA shows far better agreement with NRG results compared to IPT (See figure below).
The work has been published in Phys. Rev. B 94, 045106 (2016). A free version is available at arxiv.org : http://arxiv.org/abs/1412.4434.
Non-Hermitian quantum mechanics
In conventional quantum mechanics we have learned that a physical observable (quantum operator) needs to be Hermitian so that its eigenevalue becomes real and hence we have real meaningful expectation value. For example, a Hamiltonian should be Hermitian ($H=H^\dagger$) so that we always obtain real energies in a system. However, Carl Bender and Stefan Boettecher in 1998 extended the Hermiticity condition of a quantum Hamiltonian to a more generic condition namely the $\mathcal {PT}$ symmetry conservation in a Hamiltonian that ensures real eigenvalues under certain conditions. For instance, a Hamiltonian $\hat H= \hat p^2 + i\,\hat x^3$ does not alter under combined parity ($\mathcal P$) and time-reversal ($\mathcal T$) operation. A more generic Hamiltonian $\hat H=\hat p^2 + \hat x^2 (i\,\hat x)^\epsilon$ with $\epsilon$ being a real parameter ($\epsilon=0$ leads to our favorite quantum harmonic oscillator) shows the following eigenenergy plot.
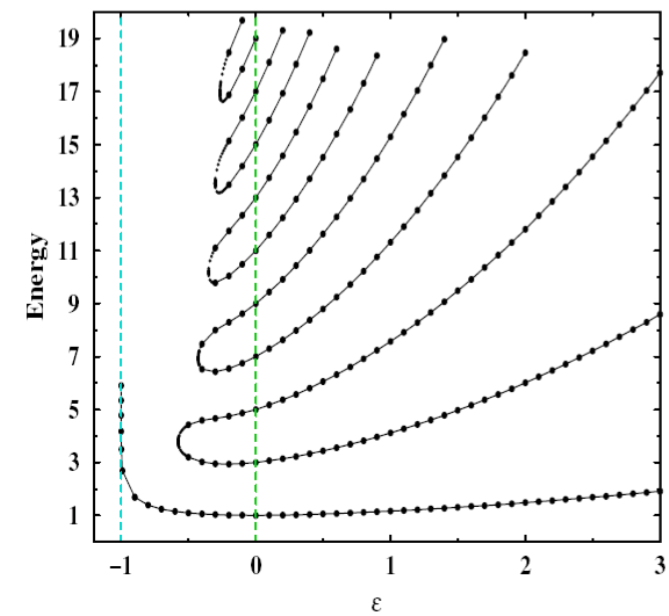
The plot shows only real eigenenergy spectra as functions of $\epsilon$. For the ground state the eigenenergy is always real and positive. It is noticed that beyond $\epsilon\lt 0$ all the eigenvalues of excited states pair up and each pair merges to a single point called the exceptional point. Beyond the exceptional points the $\mathcal {PT}$ symmetry is broken (i.e. the eigenstates no longer follows the $\mathcal {PT}$ symmetry of the Hamiltonian) and one gets purely imaginary eigen values.
Issues addressed :
- Can a dissipative Mott transition be looked from a $\mathcal PT$ symmetry breaking angle? A dissipative open quantum system (system interacting with the environment) is often described by a non-Hermitian quantum Hamiltonian. Such a situation can be imagined to a situation when an electric field induces current to one direction and leading to asymmetric hopping in a tight-binding Hamiltonian and makes it non-Hermitian. Therefore it becomes interesting to see what happens to the Hubbard model which experiences such a dissipative drive. The dissipative component of the electric field gives rise to a real phase factor ($e^\chi$) to the hopping amplitude (Peierl's term) and the Hubbard Hamiltonian looks like
$\hat H_{\text{diss}}=-t\sum_{\langle ij\rangle,\sigma}[e^\chi c^{\dagger}_{i\sigma}c_{j\sigma}
+e^{-\chi}c^{\dagger}_{j\sigma}c_{i\sigma}]-\mu\sum_{i,\sigma}c^{\dagger}_{i\sigma}c_{i\sigma}+U\sum_i \hat n_{i\uparrow} \hat n_{i\downarrow}$.
which, once reorganized, has the following $\mathcal PT$ symmetric non-Hermitian form :
We studied such Hamiltonians in 1-dimension using Bethe ansatz and higher dimensions using DMFT+IPT.
The key observations we found out of our calculations is that the energy gap ($\Delta$) in density of states
of the Mott insulating phase ($U$ sufficiently) leading to a insulator-to-metal transition, when the dissipative current crosses a critical value. The gap equation follows a universal power law : $\Delta(\lambda)=(\lambda_c-\lambda)^\nu$ where $\lambda_c$ is the critical value of $\lambda$ before the transition occurs and $\nu=$ is 0.5, 0.78, and 0.85 in 1, 2, and 3 dimensions respectively.
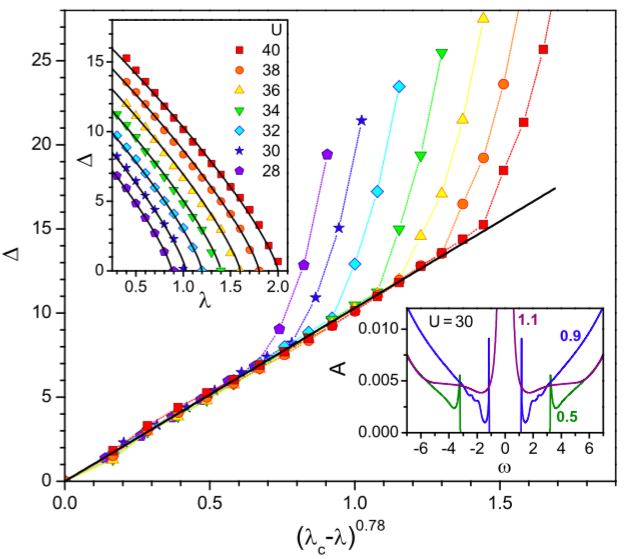
Our work has been published in , Phys. Rev. B 94, 041104 (2016). A free version is available at arxiv.org : http://arxiv.org/abs/1510.08355.