REPRESENTATION THEORY OF FINITE GROUPS

PROBLEMS SET 2

Date: July 2, 2017.

  1. Let T be a SSYT of shape μ and type λ. Let μ(i) be the subshape of λ occupied by boxes containing numbers 1,…,i. By appending trailing zeroes (if necessary), write μ(i) as a vector:
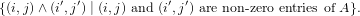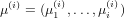
    (i) (i) μ(i) = (μ 1 ,...,μi )

    with i coordinates in decreasing order. The triangular array (μj(i)), 1 = 1,…,l, j = 1,…,i is called the Gelfand-Tsetlin pattern of T.

    1. Show that μj(i) ≥ μj(i-1) ≥ μj+1(i) for all appropriate indices i and j.
    2. Express the type of T in terms of its Gelfand-Tsetlin pattern.
  2. Interpret our algorithm for constructing a SSYT of shape μ and type λ when μ ≤ λ in terms of Gelfand-Tsetlin patterns. Extend the result about the existence of SSYT to Gelfand-Tsetlin patters with non-negative real coordinates.
  3. For each 0 ≤ k ≤ 4, how many involutions does S4 have with k fixed points? How many standard tableaux of of size 4 exist with k odd columns? Verify the second assertion about the RSK correspondence given in class.
  4. For arbitrary positive integer k ≤ n, derive a formula for the number of involutions in Sn with k fixed points.
  5. Given three positive integers a, b, and c, find a formula for M(a,b,c),(1,…,1), the number of 3 ×n matrices (where n = a + b + c) whose rows add up to a, b and c, and whose column sums are all 1.
  6. For any two elements x and y of a partially ordered set, x∧y (the greatest lower bound, or the meet of x and y) is defined as the maximal element of the set
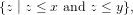
    {z | z ≤ x and z ≤ y},

    provided that such an element exists, and is unique.

    1. What is (i,j) ∧ (i′,j′) in the shadow partial order?
    2. Show that the shadow points of A are the maximal elements of the set
      ′ ′ ′ ′ {(i,j)∧ (i,j) | (i,j) and (i ,j) are non -zero entries of A }.