1If n is an integer having binary expansion n = ϵ+2k1+2k2+ +2kr,ϵ ∈{0,1},0 < k1 < k2 <
+2kr,ϵ ∈{0,1},0 < k1 < k2 <  < kr,
the number of chiral partitions of n is 2k2+
< kr,
the number of chiral partitions of n is 2k2+ +kr
+kr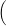 2k1-1 +∑v=1k1-12(v+1)(k1-2)-
2k1-1 +∑v=1k1-12(v+1)(k1-2)-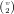 +ϵ2
+ϵ2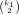
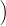 ;
see Ayyer, Prasad, and Spallone, JCTA, vol. 150, 2017.
;
see Ayyer, Prasad, and Spallone, JCTA, vol. 150, 2017.
1If n is an integer having binary expansion n = ϵ+2k1+2k2+ +2kr,ϵ ∈{0,1},0 < k1 < k2 <
+2kr,ϵ ∈{0,1},0 < k1 < k2 <  < kr,
the number of chiral partitions of n is 2k2+
< kr,
the number of chiral partitions of n is 2k2+ +kr
+kr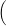 2k1-1 +∑v=1k1-12(v+1)(k1-2)-
2k1-1 +∑v=1k1-12(v+1)(k1-2)-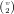 +ϵ2
+ϵ2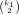
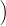 ;
see Ayyer, Prasad, and Spallone, JCTA, vol. 150, 2017.
;
see Ayyer, Prasad, and Spallone, JCTA, vol. 150, 2017.