 ) be a partition (written as an infinite list, with all
but finitely many entries zero). Let m ≥ λ1,n ≥ λ1′. Show that the
m + n numbers
) be a partition (written as an infinite list, with all
but finitely many entries zero). Let m ≥ λ1,n ≥ λ1′. Show that the
m + n numbers
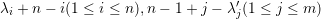
are a permutation of {0,1,2, ,m + n - 1}.
,m + n - 1}.
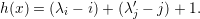
The content of x is defined to be c(x) = j - i. Prove that
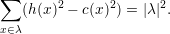
- Show that the set
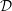 (m) of strictly decreasing m-tuples of
nonnegative integers is in bijection with the set of partitions with
at most m parts under the map λ
(m) of strictly decreasing m-tuples of
nonnegative integers is in bijection with the set of partitions with
at most m parts under the map λ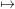 λ† where λi† = λi - (m - i)
for all i.
λ† where λi† = λi - (m - i)
for all i.
- Let λ ∈
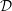 (m), 1 ≤ i ≤ m and p ≥ 1. Define uj = λj for j≠i, and
ui = λi - p. Assume that the {uj : 1 ≤ j ≤ m} are all distinct,
non-negative integers. Let μ ∈
(m), 1 ≤ i ≤ m and p ≥ 1. Define uj = λj for j≠i, and
ui = λi - p. Assume that the {uj : 1 ≤ j ≤ m} are all distinct,
non-negative integers. Let μ ∈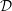 (m) denote the tuple obtained
by rearranging the uj in descending order. Describe the image μ†
of μ under the above bijection.
(m) denote the tuple obtained
by rearranging the uj in descending order. Describe the image μ†
of μ under the above bijection.
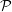 (n) denote the set of partitions of n, and ℕ the set of positive
integers. For each r ≥ 1, let
(n) denote the set of partitions of n, and ℕ the set of positive
integers. For each r ≥ 1, let
| a(r,n) | = #{(λ,i) ∈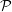 (n) × ℕ : λi = r} (n) × ℕ : λi = r} | ||
| b(r,n) | = #{(λ,i) ∈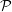 (n) × ℕ : mi(λ) ≥ r} (n) × ℕ : mi(λ) ≥ r} |
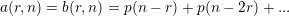
where p(m) is the number of partitions of m. Deduce that
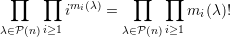
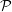 (n),x ∈ λ and h(x) = r},
where h(x) is the hook-length of λ at x. Show that h(r,n) = ra(r,n).
(n),x ∈ λ and h(x) = r},
where h(x) is the hook-length of λ at x. Show that h(r,n) = ra(r,n).