Cellular Automata

``Computation and formal language theory may in general be expected to play a role in the theory of non-equilibrium and self-organizing systems analogous to the role of information theory in conventional statistical mechanics. ''

My interest in cellular automata (CA) is an offshoot of my general interest in the problem of how complexity arises in different (natural or artificial) physical systems. In particular, cellular automata provides an ideal model system in which to study the connection between dynamics and computation - invloving inputs from nonlinear dynamical systems theory, non-equilibrium statistical mechanics and the theory of computation. At present, I am involved in the study of the complexity of computational problems in one-dimensional cellular automata - and trying to see how that relates to the dynamical complexity seen in the time evolution of CAs.

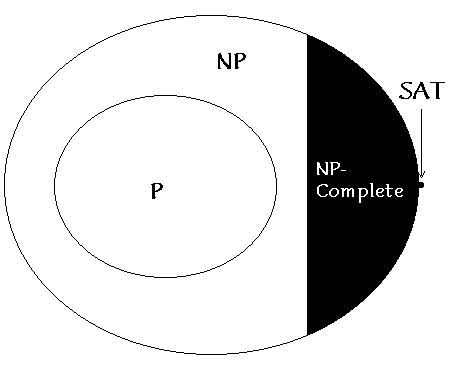
One of the main problems in studying dynamical ``complexity'' is that there is no well-defined, unambigous way to quantify it. In CAs, several measures, such as information entropy, mutual information, etc. have been used - but they are all ad hoc. Computer scientists, on the other hand, have had a well-accepted definition for complexity for a long time. They look at how the computational resources required to solve a problem scales with the size of the problem input, measured in bits. On this basis, computational problems have been divided into various classes. For our purpose, we may consider only 3 classes : P, NP and NP-complete.

P: Problems solvable in time which increases as a polynomial function of the problem size, N.
Example 1: Greatest common divisor of two integers. Euclid's algorithm solves this problem in time linear in N.
Example 2: Shortest path problem, i.e., determining whether a path of length at most k, exists between a pair of nodes of a graph of size N. The fastest algorith to solve this problem requires time O(N³).

NP: Problems solvable in time which increases faster than polynomial in N, but once the solution is obtained, it can be verified in time polynomial in N.
Example: Integer factorization problem, i.e., decomposing an ineteger into two factors.

NP-complete: Problems in NP, to which all other problems in NP can be reduced in polynomial time.

An example of an NP-complete problem is ``satisfiability'' (SAT): finding truth values for N variables which make a particular Boolean expression true. Now, the thing that got me really interested was that recently, phase transition phenomena have been reported in such computational problems. For an extremely readable account of the recent work on K-SAT, see Brian Hayes, "Can't get no satisfaction", American Scientist, Vol. 85 (2), March-April 1997.

Fig. 1a: Transition from satisfiable to unsatisfiable gets steeper as the number of variables increases. Each dot is the average of 300 problem instances.	Fig. 1b: Peak in the cost of finding solutions also gets sharper as the number of variables rises. Each dot is the average of 300 problem instances.

Finding the successor of a length N sequence in a cellular automaton takes (at most) a time linear in N. The problem of finding a pre-image for a length N sequence under cellular automaton evolution is in the class NP. it is likely that the problem of finding pre-images for sequences in certain cellular automata, or of determining whether particular sequences are ever generated, is NP-complete [1]. This would imply that no simple description exists even for some finite time properties of cellular automata: results may be found essentially only by explicit simulation of all possibilities.

Consider the generation of finite sequences of symbols in the evolution of infinite configurations. Enumeration of sets of length N sequences that can and cannot occur provide partial characterizations of sets of infinite configurations. However, even for configurations generated at a finite time t, such enumeration in general requires large computational resources. A symbol sequence of length N appears only if at least one length N₀ (= N+ 2 r t) initial block evolves to it after t time steps. A computation time polynomial in N and t suffices to determine whether a particular candidate initial block evolves to a required sequence. The problem of determining whether any such initial block exists is therefore in the class NP. One may expect that for many cellular automata, this problem is in fact NP-complete. (The procedure of Sect. 2 provides no short cut, since the construction of the required DFA is an exponential computational process.) It may therefore effectively be solved essentially only by explicit simulation of the evolution of all exponentially-many possible initial sequences.

In the limit of infinite time, the problem of determining whether a particular finite sequence is generated in the evolution of a cellular automata becomes in general undecidable.

[1] Stephen Wolfram, ``Computation Theory of Cellular Automata'', Comm. Math. Phys., 96 (1984) 15-57.