For the time-evolution generated by the time-dependent Hamiltonian
The talk discusses the Lyaponuv Center Theorem (1907), and its
recent version (1973, 1976), and an analogy with the KAM theory
for resonant tori for both finite degree of freedom dynamical
systems, and for Hamiltonian PDE. Classically, resonances
are problematic in KAM theory, and near-resonances
give rise to the small small-divisor phenomena. I described the
applications of the ideas of Fröhlich and Spencer to the
analysis of this class of problems.
For the time-evolution generated by the time-dependent
Hamiltonian
![]() , with
rotating potential with sufficiently fast decay, we prove
asymptotic completeness and asymptotic conservation of
, with
rotating potential with sufficiently fast decay, we prove
asymptotic completeness and asymptotic conservation of
![]() under scattering.
under scattering.
In addition, the kinetic energy remains bounded so that the tools of geometric scattering theory are applicable. We study the transfer of energy from the rotating body to the scattered particles for various configurations yielding an effective acceleration of the particles in a thin gas.
If ![]() and
and ![]() are bounded operators on a Hilbert space,
are bounded operators on a Hilbert space,
![]() . This was extended by Deift to the
case when
. This was extended by Deift to the
case when ![]() is a densely defined, closed operator on
is a densely defined, closed operator on ![]() ,
with
,
with ![]() , and then applied to the Strum
Liouville operator
, and then applied to the Strum
Liouville operator
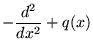 , and to the KdV equation
, and to the KdV equation
![]() .
.
We give an extension of this idea of factorization
and commutation to a large class of nonlinear evolution equations.
The corresponding eigenvalue problems include the AKNS
system for ![]() matrices, the Boussinesque
equation, the KP equations,
matrices, the Boussinesque
equation, the KP equations, ![]() -dimensional Davey Stewartson
equations, and discrete analogues, including the 2-dimensional
Toda Lattice.
-dimensional Davey Stewartson
equations, and discrete analogues, including the 2-dimensional
Toda Lattice.
A linear algebraic method for analysing the spectra of bounded self-adjoint operators on separable Hilbert spaces is presented. There are some improved version of some results of A. Böttcher, A. V. Chitra, and the author himself. The self-adjoint operators are assumed to come from the well-known Arveson class. It is also observed that there is some hope in predicting gaps in the essential spectrum.
The connection between the spectral shift function
and the local density of states is established with the
use of the Birman-Solomyak formula.
We develop the ![]() theory of the spectral shift function
applicable to pairs of self-adjoint operators whose difference
is in the trace ideal
theory of the spectral shift function
applicable to pairs of self-adjoint operators whose difference
is in the trace ideal ![]() for
for ![]() . Then we show how these
. Then we show how these
![]() estimates lead to so-called Wegner estimates on the density of states
with the correct volume dependence; they also
imply local Hölder continuity of the integrated density
of states. Finally we describe some models of random operators
to which these estimates apply. This is a joint
work with P. Hislop and S. Nakamura.
estimates lead to so-called Wegner estimates on the density of states
with the correct volume dependence; they also
imply local Hölder continuity of the integrated density
of states. Finally we describe some models of random operators
to which these estimates apply. This is a joint
work with P. Hislop and S. Nakamura.
We consider the Dirac operator with a long-range
potential ![]() . Scalar, pseudo-scalar, and vector
components of
. Scalar, pseudo-scalar, and vector
components of ![]() may have arbitrary power-like
decay at infinity. We introduce wave operators
whose symbols are, roughly speaking, constructed in terms
of approximate eigenfunctions of the stationary problem.
We derive and solve eikonal and transport equations
for the corresponding phase and amplitude functions.
>From the analytical point of view, our proof of the
existence and completeness of the wave operators
relies on the limiting absorption principle and radiation estimates
established in the paper.
may have arbitrary power-like
decay at infinity. We introduce wave operators
whose symbols are, roughly speaking, constructed in terms
of approximate eigenfunctions of the stationary problem.
We derive and solve eikonal and transport equations
for the corresponding phase and amplitude functions.
>From the analytical point of view, our proof of the
existence and completeness of the wave operators
relies on the limiting absorption principle and radiation estimates
established in the paper.
In this talk, we discuss the Lifshitz singularity of the integrated density of states for Schrödinger operators with random magnetic field. We consider 2-cases:
(1) Discrete Schrödinger operator onwith Anderson type random magnetic field;
(2) Schrödinger operator onwith metrically transitive random magnetic field.
In both cases, we show the usual Lifshitz singularity holds, in the same manner as for the Schrödinger operator with random potentials. (Here we consider Schrödinger operator without scalar potentials.) The key estimates are local energy estimates, or lower bounds of the Hamiltonian. The formulation and the proof of the local energy estimates are discussed in detail.
We discuss random Schrödinger operators in ![]() of the type
of the type
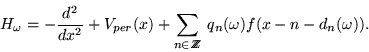
(i), i.e.
represents a (non-monotonic) displacement model;
(ii), and
has singular distribution, in particular, the Bernoulli-Anderson model where
assumes only two values.
Using the fact that the reflection coefficient of the single
site potential ![]() cannot vanish identically (in energy),
we obtain exponential and dynamical localization
at all energies for both models. In the case of dynamic
localization a discrete set of energies at which the Lyapunov exponent
vanishes has to be excluded. Similar methods allow us
to prove localization for one-dimensional Poisson models
and random operators of the type
cannot vanish identically (in energy),
we obtain exponential and dynamical localization
at all energies for both models. In the case of dynamic
localization a discrete set of energies at which the Lyapunov exponent
vanishes has to be excluded. Similar methods allow us
to prove localization for one-dimensional Poisson models
and random operators of the type
While the theory works in some generality, let us consider
a specific example of sparse random potentials:
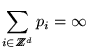 .
.
We study the homogenization of the non-linear
parabolic equation
An ordinary reflectionless potential ![]() is given by
is given by
| (1) |
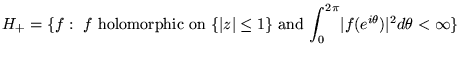 , the Hardy space on
, the Hardy space on
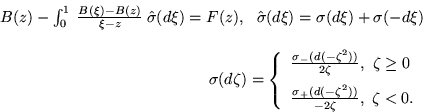
We consider the initial value problem for
the Schrödinger equation
An asymptotic formula for the density of states
of the operator
![]() in
in
![]() is
obtained. Special consideration is given to the case of the
Schrödinger equation
is
obtained. Special consideration is given to the case of the
Schrödinger equation
![]() , where the second term
of the asymptotics is found.
, where the second term
of the asymptotics is found.
We consider the random decaying model
| The Wegner Estimate, Integrated |
| Density of States and Localization |
| for Nonsign Definite Potentials |
We prove a good Wegner estimate
for various types of random operators with no sign condition
on the single-site potential. The proof yield a volume dependence
like ![]() so a consequence is the Hölder
continuity of the integrated density of states at energies
in the unperturbed spectral gap. The method
combines a vector field construction due to Klopp
and the
so a consequence is the Hölder
continuity of the integrated density of states at energies
in the unperturbed spectral gap. The method
combines a vector field construction due to Klopp
and the ![]() -estimate on the spectral shift
function due to Combes, Hislop, and Nakamura.
Under the condition that the negative part of the single
site potential is suitably small, we prove band edge localization.
-estimate on the spectral shift
function due to Combes, Hislop, and Nakamura.
Under the condition that the negative part of the single
site potential is suitably small, we prove band edge localization.
We give an account of some very recent results
on asymptotic completeness (AC) for three-body systems
with pair potentials obeying
The material presented in this talk was mainly obtained on joint work with S. Wolff to whose memory this talk is dedicated.
We consider the continuous random Anderson model in
![]() ,
where
,
where
![]() ,
, ![]() being
being
![]() periodic and
periodic and
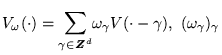 independent, identically
distributed random variables, and
independent, identically
distributed random variables, and
![]() continuous, with compact support. Let us
assume that
continuous, with compact support. Let us
assume that
![]() . Let
. Let ![]() be
the
spectrum of
be
the
spectrum of ![]() and
and ![]() be the a.s. spectrum of
be the a.s. spectrum of ![]() .
Let
.
Let ![]() be the upper edge of an open gap of
be the upper edge of an open gap of
![]() . Then, we know that the spectra are locally in the
following
relative position:
the spectra
. Then, we know that the spectra are locally in the
following
relative position:
the spectra ![]() and
and ![]() have the same lower edge
have the same lower edge ![]() and to the left of that there is a gap in both spectra.
Let
and to the left of that there is a gap in both spectra.
Let ![]() be the integrated density states of
be the integrated density states of
![]() . Then we prove
. Then we prove
Theorem 1.
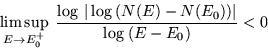
Theorem 2. For ![]() ,
,
and we compute ![]() in terms of the Newton polygon
associated
to the Floquet eigenvalues reaching the value
in terms of the Newton polygon
associated
to the Floquet eigenvalues reaching the value ![]() at the
points i.e. Floquet parameter where this value is attained.
at the
points i.e. Floquet parameter where this value is attained.
In Conne's program of Non-Commutative
Geometry, the Dixmier trace
![]() (a kind
of non-normal trace on
(a kind
of non-normal trace on
![]() vanishing on
trace-class operators) plays an important role.
In a compact Riemannian manifold
vanishing on
trace-class operators) plays an important role.
In a compact Riemannian manifold ![]() of
dimension
of
dimension ![]() , the asymptotics as
, the asymptotics as
![]() of the trace of the associated heat semigroup
of the trace of the associated heat semigroup
![]() (where
(where ![]() is the Laplace-Beltrami operator) gives various
geometric parameters of the manifold. In fact,
is the Laplace-Beltrami operator) gives various
geometric parameters of the manifold. In fact,
![]() , which by a
Tauberian theorem, equals
, which by a
Tauberian theorem, equals
![]() ,
where
,
where
![]() and
and
![]() .
It turns out that the volume form on
.
It turns out that the volume form on ![]() ,
, ![]() , is given
by
, is given
by
![]() , for
, for ![]() and
and ![]() . One establishes an identical formula for
. One establishes an identical formula for
![]() , a non-compact flat
manifold, with
, a non-compact flat
manifold, with ![]() the
the ![]() -dim
Laplacian,
-dim
Laplacian,
![]() .
A more symmetric form of this is that
.
A more symmetric form of this is that
![$ \mbox{Tr}_\omega
[ \bar{f} ( - \Delta + \epsilon )^{ - 1 } f ] =
{\displaystyle \int } \: \vert f(x) \vert^2 \: d x $](img147.png) . This implies
that
. This implies
that ![]() , the eigenvalue of the operator
, the eigenvalue of the operator
![]() , is
, is
![]() , and then leads to a connection
with a family of Schrödinger operators
, and then leads to a connection
with a family of Schrödinger operators
![]() .
.
We consider the Laplacian
 on
on ![]() -automorphic
functions
-automorphic
functions ![]() with primitive character
with primitive character ![]() . Here
. Here
![]() or
or
![]() , and
, and
![]() is a product of different primes.
The group
is a product of different primes.
The group
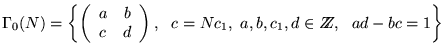 .
We give the results for
.
We give the results for ![]() , other values
of
, other values
of ![]() are similar.
The character
are similar.
The character
![]() , where
, where
![]() , for
, for
![]() , for
, for
![]() ,
and the function
,
and the function
![]() if
if
(i)The operator, the fundamental domain of
.
(ii).
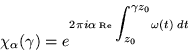
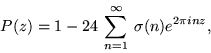
Then
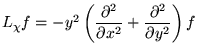 , for
, for
![]() .
.
The unitary transformation
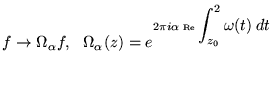 brings
brings ![]() to the form
to the form
![]() on
on
![]() -automorphic functions where
-automorphic functions where
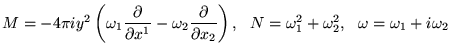 .
.
Theorem. For every odd eigenfunction
![]() of
of ![]() , which is also a common eigenfunction of all Hecke
operators, with eigenvalue
, which is also a common eigenfunction of all Hecke
operators, with eigenvalue
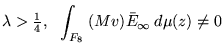 , where
, where ![]() is the Eisenstein series for the cusp at infinity. From every
eigenspace contain
ing
odd eigenfunctions with eigenvalues
is the Eisenstein series for the cusp at infinity. From every
eigenspace contain
ing
odd eigenfunctions with eigenvalues ![]() , at least
one eigenfunction
, at least
one eigenfunction
![]() of
of
![]() becomes
a resonance function of
becomes
a resonance function of ![]() .
.
Let ![]() be a self-adjoint operator, bounded
below, acting in
be a self-adjoint operator, bounded
below, acting in
![]() ,
given by a smooth increasing function of the Laplacian.
Let
,
given by a smooth increasing function of the Laplacian.
Let ![]() be a further, self-adjoint, bounded below operator.
Assume that
be a further, self-adjoint, bounded below operator.
Assume that
Under these conditions, the singular continuous spectrum of
![]() is empty.
is empty.
This abstract result is applied to generators
of ![]() -stable processes,
-stable processes,
![]() . Potential
perturbations and
perturbations by imposing boundary conditions are considered.
. Potential
perturbations and
perturbations by imposing boundary conditions are considered.
This work was due in collaboration with K. B. Sinha (Delhi), M. Bovo (Clausthal), E. Gieve (Clausthal).
| Takashi Ichinose |
| Department of Mathematics |
| Kanazawa University |
| Kanazawa, 920-1192, Japan |
The norm convergence of the Trotter-Kato product formula with optimal error bound is shown for the self-adjoint semigroup generated by that operator sum of two nonnegative self-adjoint operators which is self-adjoint.
Namely, let ![]() and
and ![]() be nonnegative self-adjoint operators
in a Hilbert space. Assume that the sum
be nonnegative self-adjoint operators
in a Hilbert space. Assume that the sum ![]() is self-adjoint on
is self-adjoint on
![]() . Then it holds that
. Then it holds that
This is based on very recent works done jointly, with Hideo Tamura (Okayama) on one hand, and with Hideo Tamura, Hiroshi Tamuya (Kanazawa), and Valentin Zaghebnov (Marseille) on the other hand.
In 1955 and 1956 Payne, Pólya, and Weinberger presented universal
inequalities for the eigenvalues of the Dirichlet Laplacian on bounded
domanins in Euclidean space. These bounds are ``universal''
in the sense that they hold for an essentially arbitrary domain, with
not even geometric data (aside from the dimension
of space, ![]() ) needing to be supplied. The prototypical
such PPW inequality is the bound
) needing to be supplied. The prototypical
such PPW inequality is the bound
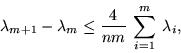
Finally, we discuss refined forms of the basic universal inequalities
that apply to bounded domains in hyperbolic space
![]() . Again, these are especially
relevant for low eigenvalues: in particular, we have the result
. Again, these are especially
relevant for low eigenvalues: in particular, we have the result
![]() for all bounded domains
in
for all bounded domains
in
![]() , improving (in two ways) upon the
result
, improving (in two ways) upon the
result
![]() of Harrell and Michel
for bounded domains in
of Harrell and Michel
for bounded domains in
![]() . The bound
. The bound
![]() derives from an even stronger and more
general inequality which we present. One of the interesting features
of the stronger bound is that it is in a certain sense sharp for domains
which are very large (think of geodesic balls with radius going
to infinity), while continuing to be quite good even down to very
small domains (where the the Euclidean behavior should predominate).
derives from an even stronger and more
general inequality which we present. One of the interesting features
of the stronger bound is that it is in a certain sense sharp for domains
which are very large (think of geodesic balls with radius going
to infinity), while continuing to be quite good even down to very
small domains (where the the Euclidean behavior should predominate).
| Andreas M. Hinz |
Since it became clear in [1] that the band structure
of the spectrum of periodic Sturm-Liouville operators
![]() does not survive a
spherically symmetric extension to Schrödinger operators
does not survive a
spherically symmetric extension to Schrödinger operators
![]() with
with
![]() for
for
![]() , a lot of detailed
information about the spectrum of such operators has been
acquired. The
observation of eigenvalues embedded in the essential spectrum
, a lot of detailed
information about the spectrum of such operators has been
acquired. The
observation of eigenvalues embedded in the essential spectrum
![]() of
of ![]() with exponentially decaying
eigenfunctions
provided evidence for the existence of intervals of dense
point spectrum, proved in [2] by spherical separation into
Sturm-Liouville operators
with exponentially decaying
eigenfunctions
provided evidence for the existence of intervals of dense
point spectrum, proved in [2] by spherical separation into
Sturm-Liouville operators
![]() .
Subsequently, a numerical approach was employed
to investigate the distribution of eigenvalues of
.
Subsequently, a numerical approach was employed
to investigate the distribution of eigenvalues of ![]() more
closely.
A Welsh eigenvalue was discovered below the essential
spectrum
in the case
more
closely.
A Welsh eigenvalue was discovered below the essential
spectrum
in the case ![]() (cf. [3]), and it turned out that there are
in
fact infinitely many, accumulating at
(cf. [3]), and it turned out that there are
in
fact infinitely many, accumulating at ![]() . Moreover, a
method
based on oscillation theory made it possible to count eigenvalues
of
. Moreover, a
method
based on oscillation theory made it possible to count eigenvalues
of ![]() contributing to an interval of dense point spectrum of
contributing to an interval of dense point spectrum of
![]() (cf. [4]). We gained evidence that an asymptotic formula, valid
for
(cf. [4]). We gained evidence that an asymptotic formula, valid
for
![]() , does in fact produce correct numbers
even for small values of the coupling constant, such that
a rather precise picture of the spectrum of radially periodic
Schrödinger operators has now been obtained.
, does in fact produce correct numbers
even for small values of the coupling constant, such that
a rather precise picture of the spectrum of radially periodic
Schrödinger operators has now been obtained.
References
[1] Hempel, R., Hinz, A. M., Kalf, H., On the Essential Spectrum of Schrödinger Operators with Spherically Symmetric Potentials, Math. Ann. 277 (1987), 197-208.
[2] Hempel, R., Herbst, I., Hinz, A. M., Kalf, H., Intervals of dense point spectrum for spherically symmetric Schrödinger operators of the type, J. London Math. Soc. (2) 43 (1991), 295-304.
[3] Brown, B. M., Eastham, M. S. P., Hinz, A. M., Kriecherbauer, T., McCormack, D. K. R., Schmidt, K. M., Welsh Eigenvalues of Radially Periodic Schrödinger Operators, J. Math. Anal. Appl. 225 (1998), 347-357.
[4] Brown, B. M., Eastham, M. S. P., Hinz, A. M., Schmidt, K. M., Distribution of eigenvalues in gaps of the essential spectrum of Sturm-Liouville operators - a numerical approach, submitted to J. Comput. Anal. Appl.
When analyzing minimizers of the Ginzburg-Landau functional
associated to a superconductive material submitted to an intense
exterior magnetic field, we meet naturally the problem
of analyzing the ground state and the corresponding
ground state energy of the Neumann realization in an open set
![]() of the Schrödinger operator with magnetic field
of the Schrödinger operator with magnetic field
![]() .
We here consider the semi-classical problem
.
We here consider the semi-classical problem
![]() and we analyze two connected questions
and we analyze two connected questions
(1) Find an expansion in powers ofof the lowest eigenvalue
(with accurate remainder estimate)
(2) Localize the ground eigenfunction as.
The results presented by the author are obtained in collaboration with A. Morame and extend previous works by us, by Baumann-Phillips-Tang, Berkoff-Sternberg, Del Pino-Föllmer-Sternberg, Lu-Pan.
In dimension 2, the main result is obtained in the case when the
magnetic field is constant. We show that
This last result is based on the following
``exercise'': Analyze as a function of
![]() , the bottom of the spectrum
of the Neumann realization in
, the bottom of the spectrum
of the Neumann realization in
![]() of the Schrödinger operator:
of the Schrödinger operator:
| Arne Jensen |
| Aalborg University, Denmark |
| and University of Tokyo, Japan |
The work presented is joint work with Michael Melgaard. In many
cases the spectrum of a Schrödinger operator has the
following
structure
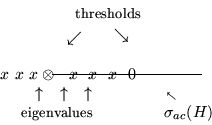
A Typical Result:
Assumptions:
(i)density and continuously such that
as, with
, in
.
(ii)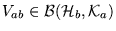
(iii)an isolated eigenvalue of
with eigenprojection
. Assume that
is strictly positive and invertible in
.
Results:
There exist
![]() ,
and a function
,
and a function ![]() satisfying
satisfying
![]() , for some
, for some ![]() , such that
, such that
The proof is based on the Feshbach formula.