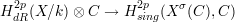8. Absolute Hodge cycles

Any projective variety X over the field of complex numbers C has as its field of definition a finitely generated (over Q) subfield k. Let [Y ] H_dR^2p(X∕k) be the cycle class of a closed subvariety of X in the algebraic de Rham cohomology of X over k (see [21] for a construction of such classes). Let σ : kC be any embedding of k in the field of complex numbers. Under the comparison isomorphism

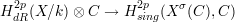
with (usual) singular cohomology, the class [Y ] maps to an integral class of type (p,p). If one is to believe the Hodge conjecture then any integral class of type (p,p) on X^σ must correspond to an algebraic cycle. It then follows that it must be in the subset H_dR^2p(X∕k) and map to an integral class of type (p,p) under any other embedding σ′. Even this (weak) consequence of the Hodge conjecture is not known and led to the definition (see [6]) of an absolute Hodge cycle.

In joint work with H. Esnault we explore the relation between this notion and the notion of absolute de Rham cycle which we have introduced. The latter is an infinitesimal analogue of the notion of absolute Hodge cycles and should prove easier to study in relation with the Hodge conjecture.

In order to make the above work complete we needed a comparison theorem between the Leray spectral sequence for algebraic de Rham cohomology and singular cohomology. While proving this a number of other applications of these homological tools were found. In particular, we were able to construct the Leray spectral sequence for de Rham cohomology, prove the comparison theorem with singular cohomology and also demonstrate the coniveau spectral sequence used (without proof) in the paper ([1]) of Bloch and Ogus.