


Next: 3 The even dimensional
Up: Continuous Self Maps of
Previous: 1.2 Computation of Homotopy
We begin by recalling the statement of Theorem 1.
Theorem 1
Let
Q be a smooth quadric hypersurface in
 n + 1
n + 1, where
n = 2
k + 1.
Then for any positive integer
d 
0 (
mod 2
k) there exist
continuous maps
f :
 n
n Q
Q, where
f*(
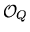
(1)) =
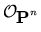
(
d ).
Proof:
This is obvious for n = 1. We may assume, by induction, that the theorem
holds for quadrics of dimension n - 2.
 n has a cell decomposition where the skeleta are linear
projective subspaces of smaller dimension. By Scholium 1 we have
a cell decomposition of Q whose n - 1 skeleton is the projective
cone C over a smooth quadric Q' of dimension n - 2. For any
d'
n has a cell decomposition where the skeleta are linear
projective subspaces of smaller dimension. By Scholium 1 we have
a cell decomposition of Q whose n - 1 skeleton is the projective
cone C over a smooth quadric Q' of dimension n - 2. For any
d'  0 (mod 2k - 1), the induction hypothesis gives us
a map
f' :
0 (mod 2k - 1), the induction hypothesis gives us
a map
f' :  n - 2
n - 2 Q' satisfying
f'*(
Q' satisfying
f'*(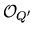 (1)) =
(1)) = 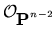 (d').
Since
(d').
Since 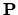 n - 1 is the projective cone over
n - 1 is the projective cone over 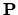 n - 2, Construction 1.1
yields a map
C(f') :
n - 2, Construction 1.1
yields a map
C(f') : 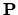 n - 1
n - 1 C.
The obstruction to extending this map to a map
C.
The obstruction to extending this map to a map 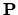 n
n Q is a class
O(C(f'))
Q is a class
O(C(f')) 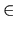 H2n(
H2n(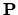 n,
n,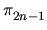 (Q)). By Lemma 4, the group
(Q)). By Lemma 4, the group
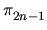 (Q) has exponent 4. Let
(Q) has exponent 4. Let 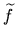 be the composite
where
be the composite
where 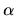 is the restriction of the map
is the restriction of the map
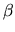 :
: 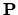 n
n
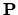 n preserving
the cell structure, and given in suitable homogeneous coordinates by
n preserving
the cell structure, and given in suitable homogeneous coordinates by
(
z0 :
... :
zn)
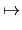
(
z02 :
... :
zn2).
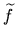 to a map
to a map 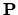 n
n Q is
Q is
O(
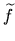
) =
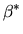
(
O(
C(
f')))
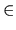 H2n
H2n(
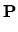 n
n,
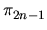
(
Q)).
But clearly 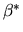 = 0 on this cohomology group.
Let
f :
= 0 on this cohomology group.
Let
f : 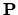 n
n Q be an extension of
Q be an extension of 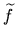 . We have a
commutative diagram of integral cohomology groups
. We have a
commutative diagram of integral cohomology groups
| H2(Q) |
 |
H2( n) n) |
  |
|
  |
| H2(Q') |
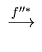 |
H2(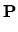 n - 2) n - 2) |
where f'' is the composite of f' with the restriction of 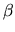 .
Since f''* is multiplication by 2d', so is f*.
.
Since f''* is multiplication by 2d', so is f*.
We now prove the following refinement of Theorem 2, in the odd
dimensional case.
1
1'
Theorem 2
Let
Q 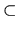
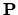 n + 1
n + 1 be a smooth quadric hypersurface with
n = 2
k + 1.
Then there exists a continuous map
f :
Q Q
Q of degree
dn whenever
- (viii)
-
d
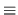 0 (mod 2k), or
0 (mod 2k), or
- (ix)
-
d = e2n - 1, for some integer e.
22
Proof:
Clearly (i) follows from Theorem 1. We prove (ii) by showing that
for the chosen integers d the map
Fd, n : Q(n + 2) Q(n + 2) extends to a map f : Q
Q(n + 2) extends to a map f : Q Q.
By induction, we may assume
that
Fd, n - 2 : Q'(n)
Q.
By induction, we may assume
that
Fd, n - 2 : Q'(n) Q'(n) extends to a map
f' : Q'
Q'(n) extends to a map
f' : Q' Q', for Q' a smooth quadric hypersurface of dimension
n - 2, and
d = e2n - 3 for some e > 0.
We have constructed (see (1.1)) a map
C(f') : C
Q', for Q' a smooth quadric hypersurface of dimension
n - 2, and
d = e2n - 3 for some e > 0.
We have constructed (see (1.1)) a map
C(f') : C C which satisfies
C(f')
C which satisfies
C(f')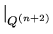 = Fd, n. By computing C(f')* on
= Fd, n. By computing C(f')* on
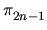 (C) we will show that the obstruction to extending
the four-fold composite C(f')4 to a self map of Q vanishes.
There is a filtration F on
(C) we will show that the obstruction to extending
the four-fold composite C(f')4 to a self map of Q vanishes.
There is a filtration F on
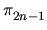 (C) given as follows.
Take
F0 =
(C) given as follows.
Take
F0 = 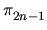 (C); F1 is the kernel of the composite
where
(C); F1 is the kernel of the composite
where 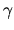 is the Hurewicz map; and finally
F2 = im (
is the Hurewicz map; and finally
F2 = im (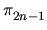 (Q(n))
(Q(n))
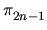 (C)).
Clearly C(f')* is compatible with this filtration and induces a
map
gr FC(f')* on
gr F
(C)).
Clearly C(f')* is compatible with this filtration and induces a
map
gr FC(f')* on
gr F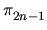 (C). This map may be
computed as follows.
(C). This map may be
computed as follows.
Lemma 6
- (x)
-
F2, F1/F2 are vector spaces over
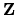 /2.
/2.
- (xi)
- The natural composite map
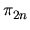
(
Q,
C)
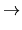
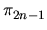
(
C)
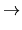 F0
F0/
F1 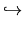 H2n - 1
H2n - 1(
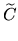
,
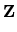
)
is an isomorphism, giving a direct sum decomposition
- (xii)
-
gr FC(f')* is multiplication by dn.
Proof:
We have a commutative diagram with exact bottom row
| |
H2n(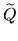 , ,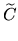 ) ) |
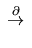 |
H2n - 1(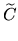 , ,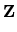 ) ) |
|
| |
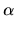 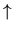 |
|
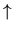  |
|
0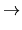 |
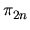 ( (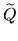 , ,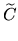 ) ) |
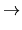 |
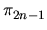 ( (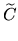 ) ) |
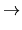 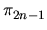 ( (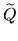 ) ) 0 0 |
The boundary homomorphism 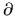 is an isomorphism by the long
exact sequence of homology for the pair
(
is an isomorphism by the long
exact sequence of homology for the pair
(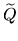 ,
,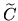 ),
and
),
and 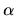 is an isomorphism by the relative Hurewicz theorem.
This proves (ii) and gives an isomorphism
F1
is an isomorphism by the relative Hurewicz theorem.
This proves (ii) and gives an isomorphism
F1 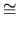
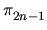 (
(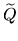 ). The self map
). The self map
 of
of
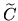 is of degree dn and this gives (iii) for F0/F1.
Since Q(n) = L is a linear projective subspace of
is of degree dn and this gives (iii) for F0/F1.
Since Q(n) = L is a linear projective subspace of 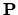 n + 1,
n + 1,
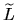 is an Sn in
is an Sn in 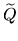 ; it is easy to check that,
in the fibration (*), this maps
isomorphically to a great sphere
S
; it is easy to check that,
in the fibration (*), this maps
isomorphically to a great sphere
S 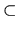 Sn + 1. In fact
Sn + 1. In fact 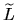 is a section of the sphere bundle of the tangent bundle of S which
is contained in
is a section of the sphere bundle of the tangent bundle of S which
is contained in 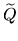 by Scholium 3.
Let D- be a hemisphere capping S in Sn + 1 and let U be its
inverse image in
by Scholium 3.
Let D- be a hemisphere capping S in Sn + 1 and let U be its
inverse image in 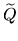 . We have the following
. We have the following
Sublemma 7
Let
i :
Sn
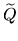
be a fibre of (*) lying over a point of
D-.
A unit tangent vector field
v on
S 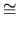 Sn
Sn
gives a map
v :
Sn
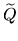
which is homotopic within
U to
the inclusion
i.
Proof:
Let p be the point of D- orthogonal to S (i.e. the ``pole'').
We have a map
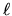 : S×[0,
: S×[0,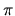 ]
] D- given by
D- given by
(
x,
t)
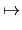
sin(
t)
. p + cos(
t)
. x.
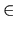 S×[0,
S×[0,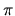 ] let n(x, t) be the tangent vector at the
point
] let n(x, t) be the tangent vector at the
point 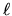 (x, t) given by
sin(t) . x - cos(t) . p. Then,
d
(x, t) given by
sin(t) . x - cos(t) . p. Then,
d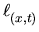 v(x) is orthogonal to n(x, t) in the tangent space of
Sn + 1 at
v(x) is orthogonal to n(x, t) in the tangent space of
Sn + 1 at 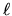 (x, t) so that we get a map
H : S×[0,
(x, t) so that we get a map
H : S×[0,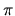 ]
]
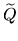 given by the formula
given by the formula
(
x,
t)
 d
d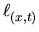 v
v(
x) + sin(
t)
. n(
x,
t).
Thus we have isomorphisms
F2 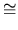 im
im (
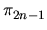
(
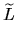
)
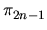
(
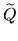
)) =
im (
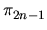
(
Sn)
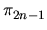
(
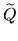
)),
where Sn Q is the inclusion of the fibre of (*). Hence
F2 is a vector space over
Q is the inclusion of the fibre of (*). Hence
F2 is a vector space over
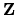 /2, and by Scholium 5
the action of
gr FC(f')* on it is by
dk + 1
/2, and by Scholium 5
the action of
gr FC(f')* on it is by
dk + 1 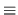 dn (mod 2). Further, we obtain an isomorphism
dn (mod 2). Further, we obtain an isomorphism
F1/
F2 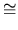
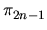
(
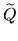
)/
im (
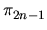
(
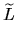
))
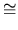 2
2(
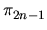
(
Sn + 1,
D-)),
so that F1/F2 is a
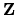 /2-vector space.
Let
g : (Dn + 1, Sn)
/2-vector space.
Let
g : (Dn + 1, Sn) (
(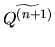 ,
,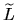 ) be the
generator of
) be the
generator of
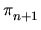 (
(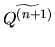 ,
,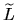 )
) 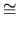
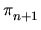 (Q(n + 1), L)
(Q(n + 1), L) 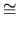
 .
We have a diagram, commutative
upto homotopy,
.
We have a diagram, commutative
upto homotopy,
| (Dn + 1, Sn) |
 |
(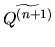 , ,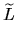 ) ) |
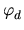 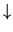 |
|
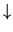  |
| (Dn + 1, Sn) |
 |
(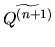 , ,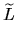 ) ) |
where 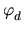 is a map of degree dk + 1. From the
Scholium 5
we see that
(
is a map of degree dk + 1. From the
Scholium 5
we see that
(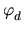 )* induces multiplication by
dk + 1 on
)* induces multiplication by
dk + 1 on
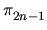 (Dn + 1, Sn).
By the sublemma we have isomorphisms
so that the composite
(Dn + 1, Sn).
By the sublemma we have isomorphisms
so that the composite
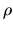 : (Dn + 1, Sn)
: (Dn + 1, Sn) (Sn + 1, D-) of
g and the natural map
(
(Sn + 1, D-) of
g and the natural map
(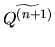 ,
,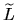 )
) (Sn + 1, D-) is also a generator
for
(Sn + 1, D-) is also a generator
for
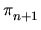 (Sn + 1, D-). By the Freudenthal suspension
theorem,
(Sn + 1, D-). By the Freudenthal suspension
theorem, 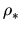 is an isomorphism on
is an isomorphism on
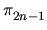 . From the
diagram
. From the
diagram
| |
H2n(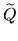 , ,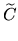 ; ;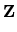 ) ) |
 |
H2n - 1(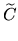 , ,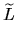 ; ;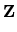 ) ) |
|
| |
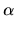 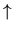 |
|
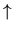  |
|
0 |
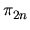 ( (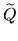 , ,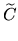 ) ) |
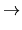 |
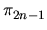 ( (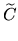 , ,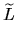 ) ) |
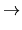 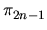 ( (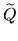 , ,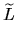 ) ) 0 0 |
where 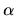 ,
,  are isomorphisms,we see that
are isomorphisms,we see that
im (
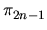
(
Dn + 1,
Sn)
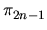
(
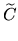
,
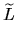
))
= ker(
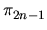
(
,
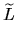
)
 H2n - 1
H2n - 1(
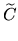
,
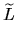
;
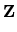
)).
In particular, F1/F2 is contained in this image; thus
C(f')* acts by multiplication by
dk + 1  dn (mod 2) on
F1/F2,and this completes the proof of (iii).
dn (mod 2) on
F1/F2,and this completes the proof of (iii).
From this lemma we see that we have
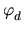
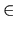 Hom (
Hom (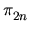 (Q, C), F1) = F1 and
(Q, C), F1) = F1 and
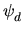
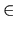 Hom (F1/F2, F2)
Hom (F1/F2, F2) 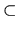 End (F1) such that, for all pairs
(a, b) in
End (F1) such that, for all pairs
(a, b) in
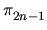 (C) =
(C) = 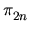 (Q, C)
(Q, C) 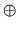 F1
we have the equation
F1
we have the equation
C(
f')
*(
a,
b) = (
dna,
dnb +
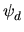
(
b) +
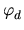
(
a)).
Since both
F1, F1/F2 are of exponent 2, it follows that the
four-fold composite of C(f') satisfies
C(f')4*(a, 0) = (d4na, 0),
and this proves the theorem.



Next: 3 The even dimensional
Up: Continuous Self Maps of
Previous: 1.2 Computation of Homotopy
Kapil Hari Paranjape
2002-11-21