Problem -99
Suppose
G is a semi-simple algebraic group over
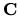
,
P 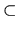 G
G a maximal parabolic subgroup,
Y =
G/
P. Let
f :
Y X
X be a finite, surjective morphism of degree > 1
to a smooth variety
X; then is
X 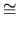
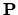 n
n?
(
n = dim
X = dim
Y)
Theorem 1
Let
Q be a smooth quadric hypersurface in
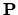 n + 1
n + 1, where
n = 2
k + 1.
Then for any positive integer
d 
0 (
mod 2
k) there exist
continuous maps
f :
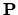 n
n Q
Q satisfying
f*(
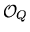
(1)) =
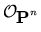
(
d ).
Theorem 2
Let
Q be a smooth quadric hypersurface in
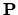 n + 1
n + 1. Then there exists
a positive integer
m and continuous maps
of degree
(
m . d )
n from
Q to
Q, for all
d 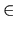
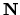
.
Y is a finite (algebraic) self map of degree > 1, then Y
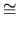
n.