


Next: Case 2: p| XYZ
Up: 2 Construction of cyclic
Previous: 2 Construction of cyclic
First of all we see easily that (X, Y, Z) are not all congruent
modulo p. If not, we have
3
X 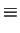 X
X +
Y +
Z 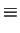 Xp
Xp +
Yp +
Zp 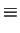
0(mod
p)
 5 and so we obtain
X
5 and so we obtain
X  0(mod p); this contradicts our hypothesis for Case 1.
Secondly, we see that
(X +
0(mod p); this contradicts our hypothesis for Case 1.
Secondly, we see that
(X +  Y) are mutually co-prime
in R as j runs over
0,..., p - 1. If not, then we have a prime
ideal P in R containing
(X +
Y) are mutually co-prime
in R as j runs over
0,..., p - 1. If not, then we have a prime
ideal P in R containing
(X +  Y, X +
Y, X +  Y). Then this
ideal P contains
(1 -
Y). Then this
ideal P contains
(1 -  )Y. Now from the factorisation
)Y. Now from the factorisation
(-
Z)
p =
Xp +
Yp = (
X +
Y)(
X +
 Y
Y)
... (
X +
 Y
Y)
 ) for
some
0
) for
some
0  l
l  p - 1. By the description of prime ideals in R as
in section 1 we see that
P =
p - 1. By the description of prime ideals in R as
in section 1 we see that
P =  R. But then Z is a multiple of
p which contradicts our hypothesis in Case 1.
By the above paragraph and unique factorization of ideals we
see that we have ideals Ij of R such that
Ijp = (X +
R. But then Z is a multiple of
p which contradicts our hypothesis in Case 1.
By the above paragraph and unique factorization of ideals we
see that we have ideals Ij of R such that
Ijp = (X +  Y)R. Assume I1 is principal; then we have an equation
Y)R. Assume I1 is principal; then we have an equation
(
X +
 Y
Y) =
u . 

 R and u a unit in R. Applying complex
conjugation we obtain
By the results mentioned in section 1 we have
R and u a unit in R. Applying complex
conjugation we obtain
By the results mentioned in section 1 we have
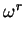
 = u for some r. Moreover,
= u for some r. Moreover,  is congruent to an
integer modulo pR and hence is congruent to its own complex
conjugate. Thus we obtain an equation
Now it follows from the description of R given in Section 1 that
it is a free abelian group with basis consisting of any (p - 1)
elements of the set
{1,
is congruent to an
integer modulo pR and hence is congruent to its own complex
conjugate. Thus we obtain an equation
Now it follows from the description of R given in Section 1 that
it is a free abelian group with basis consisting of any (p - 1)
elements of the set
{1, ,...,
,..., }. From this and
the fact that X and Y are prime to p it follows that r = 1 and
X
}. From this and
the fact that X and Y are prime to p it follows that r = 1 and
X  Y(mod p).
By similar reasoning interchanging the roles of Y and Z we can
conclude that there is an ideal J1 such that
J1p = (X +
Y(mod p).
By similar reasoning interchanging the roles of Y and Z we can
conclude that there is an ideal J1 such that
J1p = (X +  Z).
Assuming J1 is principal we see by an argument like the one above
that
X
Z).
Assuming J1 is principal we see by an argument like the one above
that
X  Z(mod p). But as seen above the two congruences
Z(mod p). But as seen above the two congruences
X 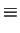 Y
Y(mod
p) and
X 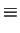 Z
Z(mod
p)
contradict the hypothesis of Case 1. Hence, either I1 or J1 must
be non-principal. But then by the principal result of Class Field
theory as mentioned in section 1 we have required cyclic extension of
K.



Next: Case 2: p| XYZ
Up: 2 Construction of cyclic
Previous: 2 Construction of cyclic
Kapil Hari Paranjape
2002-11-22