


Next: 2 Construction of cyclic
Up: Kummer's proof of Fermat's
Previous: Fermat's Last Theorem:
Let R denote the subring of complex numbers generated by
 = exp(2
= exp(2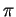
 /p); let K denote the quotient field of R,
which is called the cyclotomic field of p-th roots of unity. We
review some well-known facts about the ring R and the field
K--mostly without proof.
The ring R is isomorphic to
/p); let K denote the quotient field of R,
which is called the cyclotomic field of p-th roots of unity. We
review some well-known facts about the ring R and the field
K--mostly without proof.
The ring R is isomorphic to
 Z[X]/(
Z[X]/( (X)), where
(X)), where
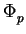
(
X) =
Xp - 1 +
... +
X + 1 = (
Xp - 1)/(
X - 1)
is an irreducible polynomial (a simple application of the Eisenstein
criterion). The field K is a Galois extension of  Q with Galois
group
Q with Galois
group
 Fp*; this is a cyclic group of order (p - 1). We use
Fp*; this is a cyclic group of order (p - 1). We use
 for a fixed choice of generator. We use
for a fixed choice of generator. We use
 to denote
to denote
 (
( ) since
) since
 is the
restriction of complex conjugation to R.
The ring R is a Dedekind domain, i. e. unique factorization holds for
ideals. The prime ideals in this ring are described as follows:
is the
restriction of complex conjugation to R.
The ring R is a Dedekind domain, i. e. unique factorization holds for
ideals. The prime ideals in this ring are described as follows:
- If
q

 Z is a prime number different from p. Then let
f be the order of q in
Z is a prime number different from p. Then let
f be the order of q in
 Fp* and let g = (p - 1)/f. Then
there are g prime ideals
Q1,..., Qg in R such that their
norms are qf.
Fp* and let g = (p - 1)/f. Then
there are g prime ideals
Q1,..., Qg in R such that their
norms are qf.
- The element
 = 1 -
= 1 -  is prime in R and
is prime in R and
 = (unit) . p.
= (unit) . p.
A closed form expression for the generators of the group U of units
of R is not known. However, the numbers
are in R and are units there. The subgroup
Ucycl of the
group U of units of R generated by the uj for
j = 2,...,(p - 1)
is called the group of cyclotomic units. If u is a unit in R,
then
 /u is a root of unity in R. The roots of unity in
R are all of the form
±
/u is a root of unity in R. The roots of unity in
R are all of the form
± for some
j = 0,..., p - 1. An
element of R is a p-th power only if it is congruent to an integer
modulo pR. It follows that
for some
j = 0,..., p - 1. An
element of R is a p-th power only if it is congruent to an integer
modulo pR. It follows that
 /u =
/u =  for some j
(i. e. there is no minus sign).
Let L denote the subfield of K fixed by complex conjugation; let
S = L
for some j
(i. e. there is no minus sign).
Let L denote the subfield of K fixed by complex conjugation; let
S = L  R. Then L is a Galois extension of
R. Then L is a Galois extension of  Q with Galois group
Q with Galois group
 Fp*/{±1}. No complex embeddings of K have image within
real numbers while all complex embeddings of L have image within
real numbers; in other words, K is purely imaginary and L is
totally real. Again, S is a Dedekind domain and its ideals are
described as follows:
Fp*/{±1}. No complex embeddings of K have image within
real numbers while all complex embeddings of L have image within
real numbers; in other words, K is purely imaginary and L is
totally real. Again, S is a Dedekind domain and its ideals are
described as follows:
- If
q

 Z is a prime number different from p. Then let
f' be the order of q in
Z is a prime number different from p. Then let
f' be the order of q in
 Fp*/{±1} and let
g' = (p - 1)/2f'. Then there are g' prime ideals
Q1,..., Qg in
R such that their norms are qf'.
Fp*/{±1} and let
g' = (p - 1)/2f'. Then there are g' prime ideals
Q1,..., Qg in
R such that their norms are qf'.
- The element
 = 1 - (
= 1 - ( +
+  ) is prime in R and
) is prime in R and
 = (unit) . p.
= (unit) . p.
If u is a unit in R, then we have seen that
 /u =
/u = 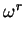 for some integer r. But then
r
for some integer r. But then
r  2s(mod p) for some integer s; hence
u1 =
2s(mod p) for some integer s; hence
u1 =  u is in
S. Hence, any unit in R is the product of a root of unity and a
unit in S.
If I is any ideal in S then IR is principal in R if and only
if I is principal in S. Hence the homomorphism from the class
group of S to that of R is injective. In particular the order h
of the class group of R is divisible by the order h+ of the
class group of S.
If we have a unit u in R such that it is congruent to an integer
modulo pR and if u is itself not a p-th power, then the
field extension of K obtained by adjoining a p-th root of u is a
cyclic extension of K of order p which is unramified everywhere.
Finally we have a fact from Class Field theory. If there is an ideal
I in R such that Ip is principal and I is not principal, then
there is a cyclic entension of K of order p which is unramified
everywhere. This follows from the identification of the class group of
R with the Galois group of the maximal unramfied abelian extension
of K. Now we use the fact that if an abelian group has an element of
order p, then it has a non-trivial character of order p.
u is in
S. Hence, any unit in R is the product of a root of unity and a
unit in S.
If I is any ideal in S then IR is principal in R if and only
if I is principal in S. Hence the homomorphism from the class
group of S to that of R is injective. In particular the order h
of the class group of R is divisible by the order h+ of the
class group of S.
If we have a unit u in R such that it is congruent to an integer
modulo pR and if u is itself not a p-th power, then the
field extension of K obtained by adjoining a p-th root of u is a
cyclic extension of K of order p which is unramified everywhere.
Finally we have a fact from Class Field theory. If there is an ideal
I in R such that Ip is principal and I is not principal, then
there is a cyclic entension of K of order p which is unramified
everywhere. This follows from the identification of the class group of
R with the Galois group of the maximal unramfied abelian extension
of K. Now we use the fact that if an abelian group has an element of
order p, then it has a non-trivial character of order p.



Next: 2 Construction of cyclic
Up: Kummer's proof of Fermat's
Previous: Fermat's Last Theorem:
Kapil Hari Paranjape
2002-11-22