6 Chow groups and Abelian varieties

For any smooth projective variety we can form a countable collection of projective schemes Hilb_n (the Hilbert or Chow schemes) that parametrise effective cycles of codimension p on X. Let C(X) be a subgroup of $\CH^{p}_{}$(X). A homomorphism of groups from C(X) to the group of rational points of a group variety A is called regular if for any non-singular variety H parametrising cycles on X lying in C(X), the resulting set maps from the set of rational points on H to the set of rational points of A is induced by a morphism of varieties.

In analogy with the picture for divisors one may ask the following questions:

1. Is there a finitely generated group N(X), a surjective map $\xi$ : $\CH^{p}_{}$(X)$\to$$\to$N(X), and a regular map from C(X) = ker$\xi$ to the group of points on an Abelian variety A, so that any regular map from C(X) to an Abelian variety factors through A?
2. Does this induce an isomorphism of $\CH^{p}_{}$(X) with N(X)×A(k)?
   (Here A(k) denotes the group of k-rational points of A.)
3. Is there a variety (or scheme) H parametrising effective cycles on X so that the morphism H$\to$A is surjective? Or at least can we arrange $\im$H = $\im$$\CH^{p}_{}$(X)?

There is no general geometric construction of the required Abelian variety. There is a complex torus associated to codimension p cycles, defined by Griffiths, which generalizes the Picard and Albanese varieties. This is called the pth intermediate Jacobian of X, and is defined by

J^p(X) = $${\frac{\HH^{2p-1}(X,{\Bbb C})}{F^p\HH^{2p-1}(X,{\Bbb C})+\im\HH^{2p-1}(X,{\Bbb Z})}}$$.

Here

F^p$$\HH^{2p-1}_{}$$(X,$$\Bbb$$C) = $$\oplus_{p'\geq p}^{}$$ $$\HH^{p',2p-1-p'}_{}$$(X)

is the pth piece of the Hodge filtration of $\HH^{2p-1}_{}$(X,$\Bbb$C). We can take the map $\xi$ : $\CH^{p}_{}$(X)$\to$$\HH^{2p}_{}$(X,$\Bbb$C) and let C(X) = $\CH^{p}_{hom}$(X) = ker$\xi$ as before. There is a map, which Griffiths calls the Abel-Jacobi map,

$$\CH^{p}_{hom}$$(X)$$\to$$J^p(X).

However, this does not have as good properties as the Picard and Albanese maps, in general. The image of $\CH^{p}_{alg}$(X) is an Abelian subvariety of J²(X) whose Lie algebra is contained in $\HH^{p-1,p}_{}$(X) $\subset$ $\HH^{2p-1}_{}$(X, C)/F^p($\HH^{2p-1}_{}$(X,$\Bbb$C).

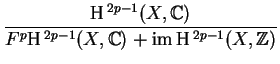The Griffiths group $\Griff^{p}_{}$(X) is always countable, since all effective algebraic cycles of a fixed degree are parametrized by the points of a (possibly reducible) Chow variety of X; taking the union over all degrees, all effective algebraic cycles lie in a countble collection of connected algebraic families, so that $\CH^{p}_{}$(X)/$\CH^{p}_{alg}$(X) is countable. Hence if $\HH^{i,2p-1-i}_{}$(X) $\neq$ 0 for some i > p, then the Abel-Jacobi map cannot be surjective. The restriction of the Abel-Jacobi map to $\CH^{p}_{alg}$(X) is a regular homomorphism onto the Abelian variety which is its image; conjecturally, this is the universal regular homomorphism, as in the case of the Albanese map. One also expects the Abel-Jacobi map to be injective on torsion, in general. The injectivity of the Abel-Jacobi map on torsion is known for codimension 2 cycles, from work of Merkurjev and Suslin on the K-theory of division algebras, combined with results of Bloch and Ogus; we discuss this below. The universality of the Abel-Jacobi map on $\CH^{2}_{alg}$(X) has been proved by Murre [27] using the injectivity on torsion.