


Next: Putting co-ordinates
Up: Foundations of geometry
Previous: Axiom of Parallels
One way of checking the consistency of our system of axioms is to
construct ``models'' for which all the axioms are verified. Of course,
these verifications again use results from some other area of
mathematics and the axioms of that would also have to be verified to
be consistent and so on. This is the idea behind the impossibility of
verifying consistency. Leaving philosophical studies behind let us
examine ``three dimensional projective geometry over a (skew-)field''.
Exercise 4
Let K be a skew-field (i.e. K has addition, subtraction,
multiplication and division but multiplication
does not necessarily commute). Points, lines and planes of
P3(K) are given by (left) linear subspaces of K4 of rank 1,
2 and 3 respectively. The incidence relations are just the inclusions
of subspaces. Show that this gives a system that satisfies the above
Incidence axioms and the projective axiom of
parallels.
In fact, this even leads to another system which satisfies the usual
axiom of parallels.
Exercise 5
Let
A3(
K) be the collection of all points, lines and planes in
P3(
K) that are not contained in a fixed plane
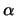
(called the
plane ``at the horizon''). Show that this geometry satisfies all
the axioms of incidence and the ``usual'' axiom of parallels.
The notion of between-ness can also be brought in with some more
algebra.
Definition 1
A positivity on
K is a subset
P so that:
-
P + P
 P and
P . P
P and
P . P  P.
P.
-
P
 {0}
{0}  (- P) = K and this is a disjoint union.
(- P) = K and this is a disjoint union.
This conforms to the concept of positive numbers. Using this we can
define the cone generated by a collection of vectors in K4 as the
collection of all non-negative linear combinations of the
vectors.
Exercise 6
Fix a three dimensional linear subspace V
of K4 (in other words a plane in P3(K)) and a vector v not in V. There is a unique linear functional on K4 which
has kernel V and takes the value 1 on v. We say a vector w is
positive if f (w) lies in P. Every linear subspace in K4
which does not line in V is then determined by its positive
half.
Exercise 7
We say that a point A of A3(K) lies between points
B and C if the positive half of the linear subspace in K4
corresponding to A is a positive linear combination of of the
positive halves of the linear subspaces corresponding to B and C
respectively. Check that the axioms of order are satisfied on A3(K)
with this notion of between-ness.
We have thus constructed a geometry satisfying all our axioms by
making use of some algebra. Other geometries satisfying these axioms
can also be constructed.
Definition 2
A collection R of points in A3(K) is said to be
convex if, given A and B are points in R and C in
A3(K) is between A and B, then C is also in R.
Definition 3
A convex collection R of points is said to be open if for any point A in R and B in A3(K), there is a
point C lying between A and B in A3(K) so that C is also in
R.
Exercise 8
Let R be an open convex collection of points in
A3(K). We denote by [R] the geometry for which points are the
points of R, lines and planes of [R] are the lines and planes of
A3(K) which meet R. The relations of incidence and order are
inherited from A3(K). Check that this geometry satisfies the axioms
of incidence and order.
A very important result (a sketch of proof is outlined in the next
section) is that every geometry satisfying the axioms of
incidence and order is of the type [R] for an open convex set R in
A3(K) for a suitable ordered field K.
Hence, and this is important to note, the fact that
arithmetic/algebraic problems arise in geometry does not immediately
have anything to do with measurement! In particular, the relation
between distance and coordinates can be much more complicated than
that which will emerge from the Pythagoras theorem.



Next: Putting co-ordinates
Up: Foundations of geometry
Previous: Axiom of Parallels
Kapil H. Paranjape
2001-01-20