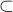 Rn+m. We obtain a graded ring
Rn+m. We obtain a graded ring  =
=  Rn.
Rn.
There are two ways in which the study of graded rings arises naturally out of the study
of affine schemes. Let R be a quotient of the polynomial algebra as considered
earlier. Let Rn be a filtration (increasing or decreasing) on the ring R such that
Rn . Rm 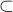 Rn+m. We obtain a graded ring
Rn+m. We obtain a graded ring  =
=  Rn.
Rn.
One way to obtain an increasing filtration on a quotient of a polynomial ring is to take Rn to the subgroup (or k vector subspace) generated by polynomials of degree at most n. This process is called homogenisation and the associated ring is denoted by Rh.
A way to obtain an increasing filtration is to take Rn = In where I is some
ideal in R. The resulting graded ring  I =
I =  In is called (for reasons that will
become clear later) the “blow-up” of Spec(R) along Spec(R/I) or of R along I for
short.
In is called (for reasons that will
become clear later) the “blow-up” of Spec(R) along Spec(R/I) or of R along I for
short.
In each case the study of the graded ring allows us to formalise (and unify) arguments by induction. However, this is not just an algebraic trick--we will see below that the constructions have a nice geometric interpretation as well.
We note that in both cases the rings obtained are quotients of the appropriate polynomial rings. The ideal generated by all the graded elements of positive degree is called the irrelevant ideal Irr(R) of such a ring. We later encounter another ideal that has “equal right” to being called the irrelevant ideal. Perhaps this should be called the “big” irrelevant ideal.
1.1. Projective Schemes. If R is a graded finitely generated ring, then consider a
morphism f : R  A such that image of the irrelevant ideal generates the unit
ideal in A. If
A such that image of the irrelevant ideal generates the unit
ideal in A. If 
 A× is a unit in A then we can modify f by defining, for each
homogeneous element x of R, (
A× is a unit in A then we can modify f by defining, for each
homogeneous element x of R, ( . f)(x) =
. f)(x) =  deg(x)f(x). Then (
deg(x)f(x). Then ( . f) : R
. f) : R  A is
again a homomorphism. If we write R as a quotient of the polynomial ring
k[X1,...,Xn,Y 0,...,Y m], with deg(Xi) = 0 and deg(Y i) > 0, by a homogeneous
ideal I, then such a homomorphism amounts to choosing elements a1,...an and
b0, ...bm in A such that they satisfy the polynomials in I and (b0,...,bm) is
the unit ideal in A. The action of units is given by replacing bi by
A is
again a homomorphism. If we write R as a quotient of the polynomial ring
k[X1,...,Xn,Y 0,...,Y m], with deg(Xi) = 0 and deg(Y i) > 0, by a homogeneous
ideal I, then such a homomorphism amounts to choosing elements a1,...an and
b0, ...bm in A such that they satisfy the polynomials in I and (b0,...,bm) is
the unit ideal in A. The action of units is given by replacing bi by  deg(Y i)bi;
since the equations are generated by homogeneous equations, this again gives a
solution.
An important example is the case where there are no X’s and no equations. The
scheme thus obtained is called the projective space of dimension m and denoted
deg(Y i)bi;
since the equations are generated by homogeneous equations, this again gives a
solution.
An important example is the case where there are no X’s and no equations. The
scheme thus obtained is called the projective space of dimension m and denoted 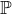 m.
More generally, we can see that all our schemes are subschemes (in fact closed
subschemes) of
m.
More generally, we can see that all our schemes are subschemes (in fact closed
subschemes) of 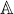 n ×
n × 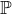 m.
m.
1.2. Segre embedding. Consider the product 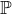 p ×
p × 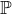 q. As a functor of points it assigns
to each finite ring A the set of pairs of tuples of the form ((a0,...,ap),(b0,...,bq)) where
the ai’s and bj’s lie in A and the ai’s generate the unit ideal as do the bj’s. It follows that
if we define cij = aibj, then we obtain a (p + 1)(q + 1)-tuple of elements of A
which also generate the unit ideal. Moreover, this tuple satisfies the collection of
equations of the form ZijZkl = ZilZkj as i,k run from 0 to p and j,l run from 0 to
q.
Conversely, let cij be a (p + 1)(q + 1)-tuple that generates the unit ideal in a finite ring
A and satisfies the above equations. We can check that each such tuple is a “product” of
a pair of tuples as above.
q. As a functor of points it assigns
to each finite ring A the set of pairs of tuples of the form ((a0,...,ap),(b0,...,bq)) where
the ai’s and bj’s lie in A and the ai’s generate the unit ideal as do the bj’s. It follows that
if we define cij = aibj, then we obtain a (p + 1)(q + 1)-tuple of elements of A
which also generate the unit ideal. Moreover, this tuple satisfies the collection of
equations of the form ZijZkl = ZilZkj as i,k run from 0 to p and j,l run from 0 to
q.
Conversely, let cij be a (p + 1)(q + 1)-tuple that generates the unit ideal in a finite ring
A and satisfies the above equations. We can check that each such tuple is a “product” of
a pair of tuples as above.
Generalising this we see that if Proj(R) and Proj(S) are two projective schemes then we can give a natural scheme structure to Proj(R) × Proj(S).
1.3. Morphisms of graded rings. If R  S is a graded homomorphism of graded
rings, then it need not give a natural trasformation Proj(S)
S is a graded homomorphism of graded
rings, then it need not give a natural trasformation Proj(S)  Proj(R). If S
Proj(R). If S  A is a
homomorphism such that the image of the irrelevant ideal Irr(S) generates the unit ideal
in A, then it need not follow that the same is true for the image of Irr(R) under the
composite homomorphism.
Suppose that S is finite as an R module. The each of the generators of Irr(S) satisfies
a monic polynomial with coefficients in R. Taking homogeneous components everywhere
we can assume that the polynomial has the form
A is a
homomorphism such that the image of the irrelevant ideal Irr(S) generates the unit ideal
in A, then it need not follow that the same is true for the image of Irr(R) under the
composite homomorphism.
Suppose that S is finite as an R module. The each of the generators of Irr(S) satisfies
a monic polynomial with coefficients in R. Taking homogeneous components everywhere
we can assume that the polynomial has the form

where the degree of rk is d(n - k) where d is the degree of the generator under
consideration. In particular, it follows that the degree of rk is positive. Thus, some power
of each generator of Irr(S) lies in the ideal Irr(R)S; hence some power of the ideal Irr(S)
lies in the ideal Irr(R)S. As a consequence, if S  A is a homomorphism such that the
image of Irr(S) generates the unit ideal then so does the image of Irr(R) under the
composite homomorphism.
A is a homomorphism such that the
image of Irr(S) generates the unit ideal then so does the image of Irr(R) under the
composite homomorphism.
We have thus shown that a graded homomorphism R  S of graded rings gives a
morphism Proj(S)
S of graded rings gives a
morphism Proj(S)  Proj(R) if the homomorphism is finite.
Proj(R) if the homomorphism is finite.
Conversely, suppose that R  S is a graded homomorphism of graded rings such that
R0
S is a graded homomorphism of graded rings such that
R0  S0 is finite and for which there is a positive integer N such that Irr(S)N is
contained in Irr(R)S. There is a a finite collection wd1, ..., wdkd of homogeneous
elements of degree d in S which generate all homogeneous elements of degree d in S over
S0. Expanding this collection as necessary and using the finite-ness of S0 over R0,
we can assume that the same generators work over R0 as well. Let e1, ..., er
denote the union of such collections for all degrees less than or equal to N.
Any homogeneous element a of S of degree greater than N can be written
as a linear combination of elements of Irr(R) with coefficients from S; such
coefficents must have degree smaller than the degree of a since elements of
Irr(R) have positive degree. By induction, we can thus write any element of S
as a linear combination over R of the e1,..., er. Hence, S is finite as an R
module.
S0 is finite and for which there is a positive integer N such that Irr(S)N is
contained in Irr(R)S. There is a a finite collection wd1, ..., wdkd of homogeneous
elements of degree d in S which generate all homogeneous elements of degree d in S over
S0. Expanding this collection as necessary and using the finite-ness of S0 over R0,
we can assume that the same generators work over R0 as well. Let e1, ..., er
denote the union of such collections for all degrees less than or equal to N.
Any homogeneous element a of S of degree greater than N can be written
as a linear combination of elements of Irr(R) with coefficients from S; such
coefficents must have degree smaller than the degree of a since elements of
Irr(R) have positive degree. By induction, we can thus write any element of S
as a linear combination over R of the e1,..., er. Hence, S is finite as an R
module.
Thus, in order that a graded homomorphism R  S be finite it is necessary
and sufficient that R0
S be finite it is necessary
and sufficient that R0  S0 is finite and that the image of the irrelevant ideal
of R generates an ideal in S that contains a power of the irrelevant ideal of
S.
S0 is finite and that the image of the irrelevant ideal
of R generates an ideal in S that contains a power of the irrelevant ideal of
S.
1.4. Homogeneous primary decomposition. Let R be a finitely generated graded
ring and Q a primary ideal in R that is not necessarily homogeneous. Let Q' be the
sub-ideal of Q generated by its homogeneous elements. We assert that Q' is primary as
well.
To prove this we can go modulo Q'; in this case we are assuming that Q is a primary
ideal such that it has no non-zero homogeneous elements. We must then show that if
fg = 0 and g is not 0, then f is nilpotent. Now if f and g are homogeneous and g is not
zero then g does not lie in Q either; by the primariness of Q, if follows that
fn must lie in it for some n and hence fn = 0. In the general case, we write
f = f0 +  + fs-1 + fs + ... and g = gr + ... where fi and gi are homogeneous
of degree i. Further suppose that s and r are chosen so that fi are nilpotent
for i < s and gr is the lowest degree term of g which is non-zero. Let N be
chosen so that (f0 +
+ fs-1 + fs + ... and g = gr + ... where fi and gi are homogeneous
of degree i. Further suppose that s and r are chosen so that fi are nilpotent
for i < s and gr is the lowest degree term of g which is non-zero. Let N be
chosen so that (f0 +  + fs-1)N = 0 and consider the binomial expansion of
(f - (f0 +
+ fs-1)N = 0 and consider the binomial expansion of
(f - (f0 +  + fs-1))Ng. The only term that does not contain fg as a factor is
(f0 +
+ fs-1))Ng. The only term that does not contain fg as a factor is
(f0 +  + f-s)Ng. Thus (fs + ...)Ng = 0; in particular, the lowest degree
term fsNgr = 0. Now applying the homogeneous case proved above we see
that fs is nilpotent as well. By induction we thus see that f is nilpotent as
required.
+ f-s)Ng. Thus (fs + ...)Ng = 0; in particular, the lowest degree
term fsNgr = 0. Now applying the homogeneous case proved above we see
that fs is nilpotent as well. By induction we thus see that f is nilpotent as
required.
Now any homogeneous ideal I in R has a primary decomposition I =  Qi. Since I is
homogeneous we see that I =
Qi. Since I is
homogeneous we see that I =  Qih as well. So that we have a homogeneous primary
decomposition of I. We shall only deal with such primary decompositions below. We
note in passing that the radical of a homogeneous ideal is also homogeneous
and so the associated and minimal primes for a homogeneous ideal are also
homogeneous.
Qih as well. So that we have a homogeneous primary
decomposition of I. We shall only deal with such primary decompositions below. We
note in passing that the radical of a homogeneous ideal is also homogeneous
and so the associated and minimal primes for a homogeneous ideal are also
homogeneous.
1.5. The “small” irrelevant ideal. Let R be a finitely generated graded ring. Let
Nk = Ann(Irr(R)k)). This is an increasing collection of homogeneous ideals for k
sufficiently large; by the Noetherian-ness condition, this sequence must terminate. Let
NR = Nk for k sufficiently large. Under any morphism R  A where the image of the
irrelevant ideal generates the unit ideal, the annihilator of any power of this ideal must
go to zero; NR must go to 0 under such a homomorphism. Thus it is truly “irrelevant”!
To summarise the “big” irrelevant ideal of R is irrelevant since under all homomorphisms
under consideration its image generates the full ring, while the “small” irrelevant ideal of
R is irrelevant since its image under all homomorphisms under considertation is
0.
Let (0) =
A where the image of the
irrelevant ideal generates the unit ideal, the annihilator of any power of this ideal must
go to zero; NR must go to 0 under such a homomorphism. Thus it is truly “irrelevant”!
To summarise the “big” irrelevant ideal of R is irrelevant since under all homomorphisms
under consideration its image generates the full ring, while the “small” irrelevant ideal of
R is irrelevant since its image under all homomorphisms under considertation is
0.
Let (0) =  iQi be a primary decomposition of the zero ideal in R. From this collection
we drop all those primary ideals that contain a power of Irr(R) (note that it is enough
that for each generator of Irr(R) there is some power which lies in an ideal for
that ideal to contain some power of Irr(R)). Let N' be the intersection of the
remaining ideals if that set is non-empty and N' = R otherwise. It is clear
that N'
iQi be a primary decomposition of the zero ideal in R. From this collection
we drop all those primary ideals that contain a power of Irr(R) (note that it is enough
that for each generator of Irr(R) there is some power which lies in an ideal for
that ideal to contain some power of Irr(R)). Let N' be the intersection of the
remaining ideals if that set is non-empty and N' = R otherwise. It is clear
that N'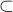 NR since N'Irr(R)l
NR since N'Irr(R)l 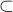
 iQi = (0) for a suitable l. Conversely, let
Qi be a primary ideal in the decomposition above that does not contain any
power Irr(R)l, then there is an i such that Y il does not lie in Qi for any l. But
Y ilNR = 0 for l sufficiently large, so NR
iQi = (0) for a suitable l. Conversely, let
Qi be a primary ideal in the decomposition above that does not contain any
power Irr(R)l, then there is an i such that Y il does not lie in Qi for any l. But
Y ilNR = 0 for l sufficiently large, so NR 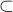 Qi. This proves that NR
Qi. This proves that NR 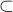 N' as
well.
N' as
well.
We note that NR = R if and only if Irr(R) is nilpotent which happens if and only if R is a finite R0 module. Moreover, these conditions imply that Proj(R)(A) is empty for all A. One we prove Hilbert’s Nullstellensatz we will show that the converse is true as well.
1.6. Homogenisation. Let R be a finitely generated ring which we think of as a
quotient of the polynomial ring with its induced filtration by degree. The associated
graded ring Rh can be thought of as the subring of R[T] whose homogeneous elements of
degree n have the form aTn, where the degree of a is at most n. The natural
homomorphism R[T]  R which sends T to 1 induces a homomorphism Rh
R which sends T to 1 induces a homomorphism Rh  R as well;
this is the dehomogenisation homomorphism.
If I is an ideal in R, then its homogenisation is the ideal J = Ih in
R as well;
this is the dehomogenisation homomorphism.
If I is an ideal in R, then its homogenisation is the ideal J = Ih in  that consists of
elements aTn with a in I. If bTn is an element of
that consists of
elements aTn with a in I. If bTn is an element of  such that bTnTm lies in J then
clearly bTn itself lies in J; in other words (J : Tm) = J for all m. Conversely, given a
homogeneous ideal J in Rh we can take its dehomogenisation I and consider Ih. If bTn is
an element of J, then b is an element of R and so bTn lies in Ih; thus J is contained in
Ih. In fact (J : Tm)
such that bTnTm lies in J then
clearly bTn itself lies in J; in other words (J : Tm) = J for all m. Conversely, given a
homogeneous ideal J in Rh we can take its dehomogenisation I and consider Ih. If bTn is
an element of J, then b is an element of R and so bTn lies in Ih; thus J is contained in
Ih. In fact (J : Tm) 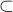 Ih for all m and Ih is the stable union of the ideals (J : Tm); the
increasing sequence (J : Tm) stops after a finite stage by the Noetherian-ness of
Rh.
Ih for all m and Ih is the stable union of the ideals (J : Tm); the
increasing sequence (J : Tm) stops after a finite stage by the Noetherian-ness of
Rh.
From this description it is clear that the homogenisation of the primary decomposition of an ideal is a primary decomposition of the homogenisation.
Let f : Rh  A be a morphism which maps the irrelevant ideal to the unit ideal. T is
an element of degree 1 in the irrelevant ideal. If T is itself mapped to a unit
A be a morphism which maps the irrelevant ideal to the unit ideal. T is
an element of degree 1 in the irrelevant ideal. If T is itself mapped to a unit  in A×,
then we can take the equivalent homomorphism
in A×,
then we can take the equivalent homomorphism  -1 . f which maps T to 1 and
thus factors through R. In other words, the elements of Proj(R)(A) that are
represented by homomorphisms Rh
-1 . f which maps T to 1 and
thus factors through R. In other words, the elements of Proj(R)(A) that are
represented by homomorphisms Rh  A that map T to a unit correspond naturally
to elements of Spec(R)(A). Thus Spec(R) can be identifed as a subscheme of
Proj(R).
A that map T to a unit correspond naturally
to elements of Spec(R)(A). Thus Spec(R) can be identifed as a subscheme of
Proj(R).
At the other extreme we can consider a homomorphism f : Rh  A that sends T
to 0 and yet maps the irrelevant ideal to the unit ideal. The multiples of T
in Rh have the form aTn where the degree of a is strictly smaller than n (so
that aTn = T(aTn-1)). All such elements must also go to 0. It follows that f
actually gives a homomorphism
A that sends T
to 0 and yet maps the irrelevant ideal to the unit ideal. The multiples of T
in Rh have the form aTn where the degree of a is strictly smaller than n (so
that aTn = T(aTn-1)). All such elements must also go to 0. It follows that f
actually gives a homomorphism  (Rn/Rn-1)
(Rn/Rn-1)  A. When R is considered as a
quotient of a polynomial ring by an ideal I and Rn is the induced filtration, this
amounts to considering the quotient of the same polynomial ring by the ideal
generated by the leading homogeneous components of elements of I. These
leading homogeneous components define the asymptotes at infinity of Spec(R).
Thus, we can think of Proj(R) as the union of Spec(R) with its asymptotes at
infinity.
A. When R is considered as a
quotient of a polynomial ring by an ideal I and Rn is the induced filtration, this
amounts to considering the quotient of the same polynomial ring by the ideal
generated by the leading homogeneous components of elements of I. These
leading homogeneous components define the asymptotes at infinity of Spec(R).
Thus, we can think of Proj(R) as the union of Spec(R) with its asymptotes at
infinity.
1.7. Blow-up. Let R be a finitely generated ring and I an ideal. Let us write R as a
quotient of the polynomial ring k[X1,...,Xn,] where the Xi generate R as a
k-algebra and Xk, ..., Xn generate the ideal I. The graded ring  I =
I =  In
(where I0 = R) can then be naturally thought of as a quotient of the graded
polynomial ring k[X1,...,Xn,Y k,...,Y n] where deg(Xi) = 0 and deg(Y i) = 1.
Moreover, we have the obvious relations XiY j = XjY i. Let K be the ideal
generated by these relations and B be Proj(k[X1,...,Xn,Y k,...,Y k]/K); the
blow-up scheme Proj(
In
(where I0 = R) can then be naturally thought of as a quotient of the graded
polynomial ring k[X1,...,Xn,Y k,...,Y n] where deg(Xi) = 0 and deg(Y i) = 1.
Moreover, we have the obvious relations XiY j = XjY i. Let K be the ideal
generated by these relations and B be Proj(k[X1,...,Xn,Y k,...,Y k]/K); the
blow-up scheme Proj( I) is a closed subscheme of B. Note that B is itself the
blow-up of the polynomial ring with respect to the ideal generated by Xk, ...,
Xn.
An element B(A) is given by taking elements a1,..., an and bk, ...bn of A such
that (bk,...,bn) generate the unit ideal in A and aibj = ajbi; in other words
(ak,...,an) and (bk,...,bn) are proportional. When A has only one maximal
ideal this amounts to saying that (ak,...,an) is a multiple of (bk,...,bn). Now, if
(ak,...,an) generate the unit ideal then multiplying factor is a unit in A and so unto
equivalence we can determine the b’s uniquely. In other words, each element of B(A)
gives an element of
I) is a closed subscheme of B. Note that B is itself the
blow-up of the polynomial ring with respect to the ideal generated by Xk, ...,
Xn.
An element B(A) is given by taking elements a1,..., an and bk, ...bn of A such
that (bk,...,bn) generate the unit ideal in A and aibj = ajbi; in other words
(ak,...,an) and (bk,...,bn) are proportional. When A has only one maximal
ideal this amounts to saying that (ak,...,an) is a multiple of (bk,...,bn). Now, if
(ak,...,an) generate the unit ideal then multiplying factor is a unit in A and so unto
equivalence we can determine the b’s uniquely. In other words, each element of B(A)
gives an element of 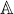 n and is point is “outside the linear subspace defined by
Xk =
n and is point is “outside the linear subspace defined by
Xk =  = Xn = 0” then the element of B(A) is uniquely determined. Here we interpret
the complement of the vanishing of the ideal as the locus where the image of the ideal
generates the unit ideal; this is not the set-theoretic complement. Similarly, the
blow-up Proj(
= Xn = 0” then the element of B(A) is uniquely determined. Here we interpret
the complement of the vanishing of the ideal as the locus where the image of the ideal
generates the unit ideal; this is not the set-theoretic complement. Similarly, the
blow-up Proj( I) of R along I has a natural map to Spec(R) which is a bijection
on the locus of maps R
I) of R along I has a natural map to Spec(R) which is a bijection
on the locus of maps R  A under which the image of I generates the unit
ideal.
A under which the image of I generates the unit
ideal.
The points of Proj( I) that map to points of Spec(R/I)
I) that map to points of Spec(R/I) 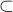 Spec(R) correspond to the
asymptotes of Spec(R) along Spec(R/I). In terms of rings we see that these are points of
Proj(
Spec(R) correspond to the
asymptotes of Spec(R) along Spec(R/I). In terms of rings we see that these are points of
Proj( (In/In-1)).
(In/In-1)).