1. Decomposition into Irreducibles

When an affine algebraic scheme Spec(R) can be written as the “categorical union” of two closed proper subschemes Spec(R/I) and Spec(R/J), we say that it is reducible; the term “categorical union” indicates the smallest closed subscheme Spec(R/K) of Spec(R) such that Spec(R/I)(A) Spec(R/J)(A) is contained in Spec(R/K)(A) for every ring A in Spec. Assuming the result that the solutions in finite rings determine the ideal, we see that reducibility is equivalent to the condition that (0) = I capJ with neither I nor J the zero ideal. Thus we can define a ring R to be irreducible if (0) cannot be written as the intersection of two non-zero ideals; an ideal I in R is irreducible if R/I is irreducible. From the Noetherian-ness of the ring R it follows that the zero ideal is a finite intersection of irreducible ideals.

There are some problems with this decomposition. First of all there is the lack of unique-ness. Secondly, the condition that an ideal is irreducible seems somewhat difficult to characterise in terms of elements. Finally, (and very importantly) the notion of categorical irreducibility seems too strong a condition to impose. For example, even the scheme Spec(k[x,y]/(x²,xy,y²) is reducible with this definition; this seems rather counter-intuitive.

Another way to decide if a scheme is irreducible is as follows. Let f and g be non-zero functions with fg = 0, then f = 0 and g = 0 would define a decomposition of the space unless f (or g is nilpotent). This corresponds to the condition that (0) is a primary ideal; an ideal Q is primary if whenever fg lies in Q and g does not lie in Q, some power of f lies in Q.

1.1. Irreducibles are primary. Let R be an irreducible ring and a be in R. If a is not nilpotent then R_a = R[T]/(aT - 1) is a non-zero ring. The kernel J of the natural homomorphism R R_a is a proper ideal. Let J = (x₁,...,x_r) (since R is Noetherian) and let n be such that aⁿx_i = 0 for all i. If y is an element of R such that a^my = 0 for some m, then y lies in J and so xⁿy = 0. Now, suppose that c lies in Raⁿ Ann(a); we have c = daⁿ and ca = daⁿ⁺¹ = 0. But then d lies in J and so c = daⁿ = 0. Since we have written (0) as an intersection of two ideals and Raⁿ is non-zero we see that Ann(a) = 0. So we have shown that every non-nilpotent element of R is not a zero-divisor. Let P be the ideal consisting of nilpotent elements. If xy lies in P then xⁿyⁿ is zero for some n, so either xⁿ = 0 or y is a zero divisor, hence nilpotent. Thus P is a prime ideal. Moreover, if xy = 0 and x does not lie in P then x is not nilpotent and so we must have y = 0. In other words, (0) is a P-primary ideal.

1.2. Irredundant primary decomposition. If P is a prime ideal in R, then the intersection of finitely many P-primary ideals in R is again a P-primary ideal. Thus, given an expression _iI_i = (0) of (0) as an intersection of irreducible ideals we can bunch together all the I_i’s which are primary for the same prime ideal. This way we obtain an expression _jQ_j = (0), where Q_j are P_j-primary for some finite collection of distinct prime ideals P_j of R. Now, we can further assume that (0) _jkQ_k for any j else we can shorten the above expression. Such an expression of (0) as an intersection of primary ideals that cannot be shortened further is called an irredundant primary decomposition of (0). Consider the ring R = k[x,y] = k[X,Y ]/(X²,XY ). We see that (0) is the intersection of the ideals RxRyⁿ for any n. This shows that we cannot home for uniqueness of the primary decomposition. However, we will see that some form of uniqueness can be proved.

1.3. Annihilators which are primary. Let Q_i = (0) be an irredundant primary decomposition of (0) and let P_i be the prime ideal which is the radical of Q_i. By irredundancy, the intersection _jkQ_j is non-zero; let c be an element of this intersection. Now suppose xy lies in Ann(c) so that xyc = 0. Thus xyc lies in Q_k, if x does not lie in P_k then yc lies in Q_k and as a multiple of c it lies in _jkQ_j as well. But then yc lies in (0) = _jQ_j and so is 0; in other words y lies in Ann(c). We have shown that Ann(c) is P_j-primary. It is also clear that Ann(c) contains Q_j. For any d not in Ann(c) consider the proper ideal Ann(dc). If xy lies in this ideal then xyd lies in Ann(c); so if x is not in P_j, then yd lies in Ann(c) (by the P_j-primality of this ideal) and so y lies in Ann(dc). In other words Ann(dc) is also P_j-primary. On the other hand, if b lies in P_j there is a positive integer n such that bⁿ⁺¹ lies in Ann(c) but bⁿ does not. Then b lies in Ann(bⁿc). Thus the maximal ideal of the form Ann(dc) must contain and thus equal P_j. We have therefore shown that prime ideals that occur in an irredundant primary decomposition of (0) in the ring R are all annihilators of some element of R.

1.4. Associated primes. The associated primes of a ring R are the prime ideals P which are of the form Ann(c) for some c in R. Suppose P is such a prime. Now consider an irredundant primary decomposition _jQ_j = (0). Among the Q_j let A be the collection of those j for which c does not lie in Q_j and let I be their intersection. If d lies in I then dc lies in all the Q_j and so must be 0; hence d lies in Ann(c) = P; so I 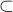P. Consider some Q_j which does not contain c; let P_j be the radical of Q_j. If d lies in P = Ann(c) then dc = 0 lies in Q_j and c does not lie in Q_j so d must lie in P_j. In other words P is contained in the intersection _jAP_j. Since P is prime it contains the radical of I which is the intersection _jAP_j. Thus P must be equal to one of the primes P_j. We have shown that the associated primes are precisely the primes that occur as the radicals of the primary ideals in an irredundant primary decomposition.

1.5. Minimal primes. A prime ideal in R that is not contained in any other prime ideal is called a minimal prime of R. Let _jQ_j be an irredundant primary decomposition of (0) in R. The radical of (0) consists of all nilpotents and is the thus the intersection of the radicals P_j’s of the Q_j’s. Since the nil radical of a ring R is contained in all the prime ideals of R it follows that the minimal primes in R are the minimal elements in the collection of the P_j’s. The minimal prime ideals of a ring R are the minimal elements in the finite collection of associated primes of the ring R. The non-minimal associated primes are called embedded primes. Let P_k be an associated prime in R and let Q be the collection of all c such that there is some d not in P such that dc = 0. For any irredundant primary decomposition _jQ_j, we see that Q is contained in Q_k. The ideal I_k = _jkQ_j is non-zero and its radical is _jkP_j. If P_k is a minimal prime then it does not contain the latter ideal and hence it does not contain I_k either. It follows that there is a d that lies in I_k but does not lie in P_k. For any c in Q_k, the element dc lies in I_k Q_k = (0) so is 0. Thus we see that Q = Q_k. The primary ideal in an irredundant primary decompostion that corresponds to a minimal prime in R is uniquely determined.

1.6. Zero-divisors in a ring. From the description given above we see that the associated prime ideals consist of zero-divisors. Conversely, if xy = 0 and x does not lie in an associated prime P_j then y must lie in the corresponding Q_j. So if x does not lie in any associated prime P_j then y lies in all the Q_j’s and so must be 0. The collection of zero-divisors in R is thus precisely the union of all its associated primes.

1.7. Some geometry. We have seen that the primary decomposition is related to the decomposition of Spec(R) into irreducibles components. If we ignore for the moment, the distinction between irreducible components which differ only in their “nilpotent thickenings”, then the primary decomposition precisely corresponds to the decomposition into irreducible components. A zero-divisor c should be seen as a function that vanishes on some components but not others; the components on which it does not vanish are defined by the vanishing of those functions d such that dc is identically the zero function; that is, Ann(c). We have seen above that for any component, there is a function c such that Ann(c) is a primary ideal associated to that component; this is a function that vanishes on all components except the chosen one. This interprepretation makes sense unless the corresponding prime ideal is embedded (i. e. non-minimal). How can a function vanish on a component but apparently not on a closed subset? What can and does happen is that the function vanishes on the larger component but is nilpotent and non-zero on the embedded component which is contained in this larger component.

The primes associated with a component consist of functions that are nilpotent on that component. The above description also leads to characterisation of functions c that vanish on a non-embedded component as those for which there is function d which is not nilpotent on this component such that dc identically vanishes.

Finally, while dealing with primary decomposition, it is easy (but erroneous) to loose track of the elements of R which are not zero-divisors. We will see these elements acquire importance in a later section.