 Spec(k[T]).
Your proof should work over any field k!
Spec(k[T]).
Your proof should work over any field k!
...bend down and touch the floor. I have collected a bunch of what I think are instructive exercises.
1.1. Finite Rings. Give a structure theorem for finite rings of order p3. Is it possible to “easily” generalise this for pn for all n?
1.2. Hensel’s lemma. Use Hensel’s lemma to show that any matrix A over a field of characteristic 0 can be written as the sum A = S + N with S and N commuting with each other, N nilpotent and the minimal polynomial of S is separable (“has distinct roots”). Can you generalise this to characteristic p?
1.3. Affine schemes. Show that there cannot be an isomorphism between Spec(k[X,Y ]/(X2 - Y 3)) and Spec(k[T]) by considering these as functors on the category of finite dimensional k algebras.
1.4. Finite morphisms. Find a finite morphism Spec(k[X,Y ]/(XY (X +Y )-1))  Spec(k[T]).
Your proof should work over any field k!
Spec(k[T]).
Your proof should work over any field k!
1.5. Closed morphisms. Show that the morphism Spec(k[X,Y ])  Spec(k[X]) is not
closed.
Spec(k[X]) is not
closed.
1.6. Hilbert basis theorem. Consider the ideals defining circles with centres along points of the y-axis. What is a finite basis for the ideal defining the intersection of the corresponding closed subschemes?
1.7. Primary decomposition. Let Spec(R/I) be a closed subscheme of a scheme Spec(R). If I is contained in a component of Spec(R) then show that every element of I is a zero=divisor. What about the converse?
1.8. Segre embedding. Consider the natural transformations of functors
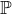 n ×
n × 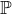 m
m 
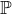 nm+n+nm which, for each finite ring A, has the form
nm+n+nm which, for each finite ring A, has the form
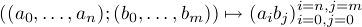
Show that this is a bijection onto the projective variety in 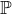 nm+n+m defined by the
equations ZijZkl = ZilZkj as i, k (respectively j, l) vary from 0 to n (respectively from
0 to m).
nm+n+m defined by the
equations ZijZkl = ZilZkj as i, k (respectively j, l) vary from 0 to n (respectively from
0 to m).
1.9. Empty projective schemes. Let R be a finitel generated graded ring which is a finite over the subring R0 of elements of degree 0. Show that Proj(R)(A) is empty for every finite ring A. What about the converse?
1.10. Dimension theory. Let R be a graded k-algebra with R0 = k such that the
graded dimension of R is r. Let k[Z0,...,Zr]  R be a graded homomorphism such that
it induces a morphism Proj(R)
R be a graded homomorphism such that
it induces a morphism Proj(R) 
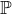 r. Show that the homomorpihsm is finite.
r. Show that the homomorpihsm is finite.