1. Two Descriptions of the Category of Affine Schemes

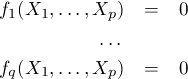
Affine algebraic geometry could be described as the study of solution of a finite system of polynomial equations in a (finite) number of variables. The objects of the category are then systems of equations of the form

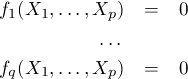
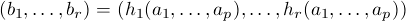
gives a solution of the second system. Moreover, two such morphisms (h₁(X₁,...,X_p),...,h_r(X₁,...,X_p)) and (h'₁(X₁,...,X_p),...,h'_r(X₁,...,X_p)) are equal if the values are equal, i. e. 

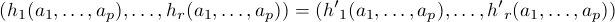
“whenever” (a₁,...,a_p) satisfy the first system of equations (f₁,...,f_q).

The crucial step is to understand the meaning of “whenever”. After all, if we only look at solution in integers or rational numbers or some finite field, then there may not be “enough” solutions to characterise the system. Thus there are three possible interpretations of this pseudo-definition.

1.1. Ring theoretic definition. In this case we assume that the interpretation of “whenever” is in the formal algebraic sense by “substitution”. Let R be the ring

where we are examining equations with coefficients in integers or Diophantine equations; when we are looking at equations with coefficients in a field k we can replace 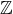by k. Clearly, a soltution in any ring (resp. k-algebra) S of the system of equations can be interpreted as a ring homomorphism (resp. k-algebra homomorphism) R S. Similarly,

A “substitution” (h₁(X₁,...,X_p),...,h_r(X₁,...,X_p)) is a ring homomorphism

The condition that it gives a morphism from the first system of solutions to the other says that g_i(h₁,...,h_r) should become zero in the quotient R of 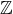[X₁,...,X_p]. In other words, this substition corresponds to a homomorphism of rings R' R. Moreover, equality of (h₁,...,h_r) with (h'₁,...,h'_r) corresponds to equality of the resulting homomorphism R' R.

The algebraic definition of the category of Affine Schemes (of finite type over 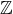or a field k) is thus the opposite category of the category of rings of the above type; note that the homomorphism of rings goes in the opposite direction! Just to avoid confusion the term Spec(R) is used when a ring is considered as an affine scheme.

1.2. An arithmetic-geometric approach. The above approach is mildly dis-satisfying to the number theorist or the geometer since it does not seem to involve the “solutions” of the equations in any way! The classical approach of looking at solutions in algebraic numbers or complex numbers is also unsatisfactory since it does not distinguish between the equation X² = 0 and X = 0 which must be distinguished for a number of reasons. Another problem with the above approach is that it does not easily generalise to more general (i. e. non-affine) algebraic schemes. One solution is to look at solutions in finite rings (for equations with coefficients in 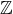) or finite dimensional k-algebras (for equations with coefficients in a field k). The latter has an interesting interpretation as rings of commuting matrices. Let Spec denote this category of rings or k-algebras as the case may be.

Any system (f₁(X₁,...,X_p),...,f_q(X₁,...,X_p)) of equations as above gives a functor from Spec to the category of sets which takes a finite ring A to the set V (f₁,...,f_q)(A) of solutions of the equations with (a₁,...,a_p) with the a_i in A. Let V (f₁,...,f_q) denote this functor. Let 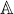^k denote the functor from Spec to sets that assigns to each finite ring A the set of all k-tuples (a₁,...,a_k) with entries in A; thus 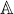^k corresponds to 0 equations in k variables! Clearly V (f₁,...,f_q) is a sub-functor of 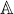^p in a natural way.

A system of polynomials (h₁,...,h_r) as above is said to give a morphism V (f₁,...,f_q) V (g₁,...,g_s) if “whenever” in the above pseudo-definition is interpreted with solutions in finite rings in A. The polynomials h_i define a natural transformation 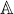^{p 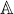r} and we have a morphism V (f₁,...,f_q)(A) V (g₁,...,g_s) if this natural transformation takes V (f₁,...,f_q)(A) to V (g₁,...,g_s)(A) for every ring A in Spec. Two morphisms (h₁,...,h_r) and (h'₁,...,h'_r) are equal if the induced maps on V (f₁,...,f_q)(A) are equal; note that this need not imply that the maps are equal on all tuples (a₁,...,a_p).

1.3. The equivalence. If R is the ring associated with the system (f₁,...,f_q) then it is clear that V (f₁,...,f_q)(A) can be identified with the ring homomorphisms R A. In particular it follows that a morphism Spec(R) Spec(R'), which can be identified with a homomorphism R' R, gives rise to a set map Hom(R,A) Hom(R',A). There is thus a natural functor from the category of Spec(R)’s to the category of V (f₁,...,f_q)’s. We need to prove that this is an isomorphism of categories. Since the objects of the two categories correspond to each other in a natural way, this proof reduces to checking the identification of the morphisms. On the one hand we need to see that given two distinct homomorphisms R' R the induced maps Hom(R,A) Hom(R',A) are different for at least one ring A in Spec. On the other hand we need to show that if (h₁,...,h_r) gives a morphism from V (f₁,...,f_q) to V (g₁,...,g_s) then it gives a homomorphism R' R.

Now let us assume the following result which will prove later. For any ring R of the type considered above the kernels, of all homomorphisms from R to a ring A in Spec, have zero as their common interesection; i. e. 

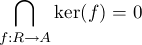
Assuming this we will be able to demonstrate what we want.

Let h = (h₁,...,h_r) be a collection of polynomials. This induces a homomorphism [Y ₁,...,Y _r] [X₁,...,X_p] (or with 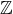replaced by k in case we are in the situation of k-algebras). To get a homomorphism R' R we need the condition that the ideal g₁,...,g_s) generated by the g_j’s is sent into the ideal (f₁,...,f_q) generated by the f_i’s; let I_h denote the image ideal. The condition that we have a morphism V (f₁,...,f_q) V (g₁,...,g_s) is the condition that every homomorphism R A vanishes on I_h. By the result we have assumed this means that the image of I_h in R is zero; in other words I_h is contained in the ideal (f₁,...,f_q) as required to obtain a homomorphism R' R.

If h and h' induce distinct homomorphisms R' R, then there is at least one i such that the image of h_i in R is different from the image of h'_i in R. Consider the non-zero element h'_i - h_i of the ring R. By the result assumed there is a homomorphism ring A in Spec and a homomorphism R A such that the image of this element in A is non-zero. In other words, the images of h_i and h'_i in A are distinct. Thus the composite induced homomorphisms from R' to A are distinct; hence the induced maps Hom(R,A) Hom(R',A) are distinct as required.

1.4. Closed morphisms. A special class of morphisms of affine schemes is Spec(R/I) Spec(R) where R R/I is the quotient by an ideal. This is called a closed subscheme; the “sub” part is because Spec(R/I)(A) 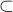Spec(R)(A) consists of those homomorphisms that vanish on I. If I and J are ideals in the ring R, then I + J is also an ideal. Clearly, an element of Spec(R)(A) that lies in Spec(R/I + J)(A) lies in Spec(R/I)(A); similarly for J. Thus the intersection of two closed subschemes is also a closed subscheme. More generally we can take the sum of any collection of ideals of R to show that the intersection of any collection of closed subschemes is a closed subscheme.

The union of closed subschemes is a more tricky affair. The union of Spec(R/I)(A) and Spec(R/J)(A) (as subsets of Spec(R)(A)) is not associated with an ideal in general. The natural ideal to consider is I J but there may be more elements in Spec(R/I J)(A) then those coming from Spec(R/I)(A) and Spec(R/J)(A); the whole is greater than the sum of the parts! However, if we restrict A to be a field then the kernel of R A is a maximal ideal (hence prime) and thus if it contains I J then it must contain either I or J. Alternatively we could look for the smallest closed subscheme (equivalently, the largest ideal K) such that it contains the union for all A; in other words, what is the largest ideal K which lies in the kernel of all homomorphisms R A that vanish on either I or J; we will later show that this is the ideal I J.

With these two definitions we see that closed subschemes satisfy the usual properties of closed-ness.

1.5. Images and inverse images. Let f : R R' be a homomorphism of rings and I an ideal in R. Given a ring homomorphism g : R' A such that the composite homomorphism R R' A vanishes on I, we see that g(f(I)S) = 0. Conversely, any homomorphism g with the latter property gives a homomorphism g o f : R A that vanishes on I. Thus the inverse image of Spec(R/I)(A) under Spec(R')(A) Spec(R)(A) is Spec(R'/(f(I)S))(A). Given any homomorphism f : R R' and a closed subscheme Spec(R'/J) of Spec(R') we could ask for its “image” under Spec(R') Spec(R). As above this is a bit tricky. One possible definition would be to take I = f^-1(J) and call Spec(R/I) its image. However, this need not always be the image in the “functorial” sense. In other words, for a finite ring A the image of the composite Spec(R'/J)(A) Spec(R')(A) Spec(R)(A) need not be Spec(R/I)(A). In fact, Spec(R')(A) Spec(R)(A) need not be surjective. We thus have the following weaker notion which is adequate.

Given a non-zero morphism R/I A with A finite, we ask for a non-zero ring homomorphism A B such that the composite R/I A B also factors as R/I R'/J B. In this case we can call Spec(R/I) the “true” image of Spec(R). In case the true image of Spec(R'/J) is Spec(R/f^-1(J)) for all ideals J in Spec(R') we say that the morphism Spec(R') Spec(R) is closed.

1.6. Finite morphisms. A special class of morphisms of affine schemes where “image” is better behaved is given by f : R S where S becomes a finitely generated R-module under f; such a morphism is called “finite”. Let x₁, ..., x_r be system of generators of S as an R module. By using this as a “basis”, to every alement a of S we can an associate an r × r matrix A with entries a_ij in R by the formula

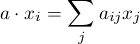
Let B be the adjoint of the matrix A-a1_r so that B(A-a1_r) = det(A-a1_r) ^.1_r. We see that det(A - a1_r)x_i = 0 for all i. Thus it is the 0 element of S. The polynomial det(A - T1_r) is a polynomial of degree r over R with leading coefficient a unit. In other words it is a monic polynomial. Thus we have seen that each element of S satisfies a monic polynomial over R; such an element is called an integral element.

Conversely, if R S is a ring homomorphism and x in S is integral over R, we see that R[x] 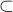S is a quotient of the finitely generated R-module R[T]/(f(T)) for some monic polynomial f satisfied by x. It is clear that finite-ness is transitive so we see that any finitely generated R-algebra S (all algebras in our current examples) such that every element is integral over R (such a ring is called an integral extension of R) is also finite over R.

Now, if J is an ideal in S then R/f^-1(J) S/J is also finite; in addition it is injective. We can now show that it is a “true” image in the sense given above. We can replace R by R/f^-1(J) and S by S/J so we have an injective finite morphism R S. Given a non-zero homomorphism R A with A finite we want to show that there is a non-zero “lift” as above. Let Q be the kernel of R A; it is enough to show that S/f(Q)S is non-zero and finite for we can then take B to be A 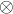_R/QS/f(Q)S. The lemma that does this is another guise of Nakayama’s lemma. Note that S/f(Q)S is finite over the finite ring R/Q and hence it is itself finite. Thus we only need to show that it is non-zero.

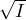We will prove the slightly more general result that follows. Let f : R S be injective and finite as above. Let I be any ideal in R, then we claim that IS R is contained in , the radical of I.

Let x₁,..., x_r be a set of generators of S as an R module. If b lies in f(I) R then we have expressions bx_i = 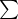_jf(a_ij)x_j with a_ij in I. But then multiplying on the left with the adjoint of the matrix b1_r - (a_ij) we see that det(b1_r - (a_ij)) acts as 0 on all the x_i. In other words b satisfies the characteristic polynomial P(T) of the matrix (a_ij), which is a monic polynomial whose coefficients, as polynomials in the a_ij, lie in I. This means that bⁿ lies in I or that b lies in 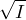as required.

1.7. Hilbert’s basis theorem. We started with a finite system of equations but then “generalised” to an arbitrary ideal. Is this truly a generalisation? Hilbert proved otherwise. In other words we claim that any ideal in the polynomial ring is finitely generated; in other words that the polynomial ring is Noetherian. The proof proceeds by induction. It is obvious that a field k (with only two ideals) is Noetherian; the Noetherian property for 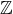follows from Euclid’s algorithm. Let R be a ring which is Noetherian, we claim that R[X] is also Noetherian. Before starting, let us note that if R S is finite then S is also Noetherian. This is because it is already Noetherian as an R module. The general case is modelled on this.

Let I be an ideal in R[X]. We want to show that this ideal is finitely generated.

If I contains a polynomial f(X) whose leading coefficient is a unit (a monic polynomial), then we note that R[X]/(f(X)) is isomorphic to R^deg(f) as an R module; thus the problem of finite generation of I/(f(X)) is reduced to the Noetherian-ness of finitely generated modules over R.

More generally, we proceed as follows. Let I[X^-1] denote the ideal generated by I in the ring R[X,X^-1]; let I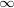 be the intersection of I[X^-1] with the subring R[X^-1] of R[X,X^-1]; then the content c(I) of the ideal I is the image of I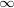 in R = R[X^-1]/(X^-1); it is also the ideal consisting of the leading coefficients of elements of I. Since c(I) is an ideal in R it is finitely generated. Let f₁, ..., f_r be elements of I whose leading coefficients generate c(I); we can assume that all the degrees deg(f_i) are equal to some fixed positive integer k by replacing f_i by a multiple of it with some power of X if necessary. 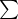If g is an element of I of degree at least k and a is its leading coefficient then, by writing a as an R-linear combination of the generators of c(I), we can find a linear combination of the form a_if_i(X)X^l which has the same leading coefficient as g; by subtracting this element from g we obtain an element of I of small degree. Hence any element of I can be written as a linear combination of the f_i and an element of I whose degree is less than k. As before the elements of I whose degree is less than k form a Noetherian module over R; we can therefore find a finite R-basis for this collection of elements. This R-basis combined with the polynomials f₁, ..., f_r then generate the ideal I.