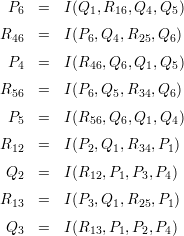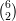A double-six consists of a pair of ordered 6-tuples of lines (P₀,…,P₅) and (Q₀,…,Q₅) such that each P_i meets all the Q_j except Q_i.

For each i and j consider the intersection of the plane spanned by P_i and Q_j with that spanned by P_j and Q_i; this gives a line R_ij which meets all the four lines. This gives us 6 + 6 + 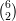= 27 lines1 .

We will construct a Shlafly double-six and write the equation of the (unique) cubic that contains it.

Let F denote the smooth quadric in ℙ³ defined by XY - ZT = 0. This contains the lines:

1. P₁ defined by X = Z = 0.
2. P₂ defined by Y = T = 0.
3. P₃ defined by X = T and Y = Z.
4. Q₄ defined by X = Z and Y = T.
5. Q₅ defined by Y = Z = 0.
6. Q₆ defined by X = T = 0.

This choice of lines means that P_i meets Q_j for i = 1,2,3 and j = 4,5,6. At the same time the P_i’s are mutually disjoint; as are the Q_j’s. Conversely, given such a collection of six lines we can always choose co-ordinates so that these lines are given by the equations above. As a consequence such a configuration always lies in a (unique) smooth quadric.

We take a general linear polynomial aT + bX + cY + dZ and consider the cubic surface S defined by the equation

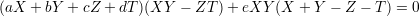
It is clear that the lines above are contained in S. Conversely, any cubic that contains the six lines defined above has this form.

We will construct the Shlafly double-six for S by suitably choosing the constants a, b, c, d, e. Now S also contains the lines:

1. R₁₆ defined by X = 0 and aX + bY + cZ + dT = 0.
2. R₂₅ defined by Y = 0 and aX + bY + cZ + dT = 0.
3. R₃₄ defined by X + Y = Z + T and aX + bY + cZ + dT = 0.

We want a line Q₁ which meets the lines P₂, P₃ and R₁₆. Since the latter three are skew lines, Q₁ is uniquely determined by its intersection with P₂ as follows. Let us pick a point x₂₁ of P₂ given by (X : Y : Z : T) = (t : 0 : 1 : 0). Let π₆₁ be the span of x₂₁ and the line R₁₆ and let π₃₁ be the span of x₂₁ and the line P₃. Then Q₁ is the line where the planes π₆₁ and π₃₁ intersect.

In order that S contains Q₁ we need to choose the constants a, b, c, d and e so that

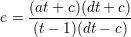
If this is done then the cubic S contains Q₁. We claim that this cubic contains a Schlafly double-six which we now construct.

We will repeatedly apply the following construction. Let L₁, L₂, M₁ and M₂ be lines in S such that:

1. L₁ and L₂ meet.
2. M₁ and M₂ do not meet either L_i or each other.

Let π be the plane containing L₁ and L₂. The intersection of S and π contains L₁ and L₂. The residual intersection is then another line L₃. The intersection of M_i with the plane π does not lie on L₁ or L₂ and hence must lie on on L₃. We can thus construct L₃ as the line joining the intersection of M₁ and π with the intersection of M₂ and π. We denote this line by I(L₁,L₂,M₁,M₂).

The inductive construction of the remaining lines in the double-six is as follows: