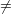An irreducible projective variety of dimension 2 is called a projective surface. We call a surface S ⊂ ℙⁿ ruled if it is covered by a family of lines. Recall that the Grassmanian 𝔾(1,n) is a projective variety parametrising lines in ℙⁿ; there is a sub-variety I ⊂ ℙⁿ × 𝔾(1,n) such that the fibre over any point of 𝔾(1,n) is a line in ℙⁿ. We thus define a ruled surface by saying that there is a curve C ⊂ G(1,n) such that S is the image p₁(p₂^-1(C) ∩ I).

We have already seen two examples in the previous lecture. The first (trivial) example is the cone. Let C be a curve in ℙ^n-1 and consider ℙ^n-1 as obtained from ℙⁿ by projecting from a point P in ℙⁿ. Let S be the closure of the inverse image of C under the morphism ℙⁿ -{P}→ ℙ^n-1. Clearly, S is a ruled surface. A slightly more interesting example is the surface Q in ℙ³ that is defined by WY - XZ = 0. As we saw in the previous lecture, this is isomorphic to ℙ¹ × ℙ¹. In fact, if A = (w : x : y : z) is any point on Q, then the tangent plane T_A to Q at A is defined by yW - zX + wY - xZ = 0. One computes that the intersection T_A ∩ Q is the union of the parametric lines (here we assume that w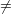0)

It follows that Q is a ruled surface in two different ways.

Now one could argue that the study of ruled surfaces is identical to the study of curves in 𝔾(2,n) for various n, but the latter approach is additionally complicated by the slightly more complicated geometry of 𝔾(2,n) as compared with the geometry of ℙⁿ. Hence, we study ruled surfaces more directly.

Consider a point A on a ruled surface S ⊂ ℙⁿ and the projection p_A : ℙⁿ -{A}→ ℙ^n-1. If L is any line in S that does not contain A, then the image of L is again a line in ℙ^n-1. Thus the closure T of the image of S -{A} is again a ruled surface providing that the image is a surface; the latter condition only fails when S is the cone over a curve in ℙ^n-1 as constructed above. When T is a surface it is not isomorphic to S; when A is a smooth point of S, the correspondence between T and S is called an elementary transformation from T to S.

Recall that the closure of the graph of p_A is an n-dimensional sub-variety 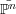_A ⊂ ℙⁿ × ℙ^n-1. The morphism 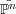_A → ℙ^n-1 identifies ℙ^n-1 as the space of lines in ℙⁿ that contain A or equivalently the space of tangent directions to ℙⁿ at A. As is obvious, any point B of ℙⁿ such that B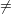A determines a unique such tangent direction (given by the line joining A and B) so that morphism 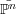→ ℙⁿ is an isomorphism outside A. On the other hand the fibre of this morphism over A is all of ℙ^n-1.

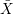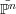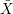If X is any irreducible variety in ℙⁿ that properly contains A, then let _A ⊂_A denote the closure of the graph of the restricted morphism p_A|_X : X -{A}→ ℙ^n-1. When X is smooth at A the fibre of _A → X over the point A can be realised as the space of tangent directions to X at A. When X is singular, this could be used to define what one can think of as the locus of lines tangent to X at A; but this is not the collection of all lines in the Zariski tangent space of X at A when X is singular at A. In order to avoid confusion, the fibre of 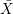_A → X was called the apparent locus of X at A in classical geometry. Its algebraic description is as the “proj” of the associated graded ring obtained from the local ring of X at A. The morphism 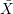_A → X is called the blow-up of X at A.

Returning to the ruled surface S, let 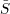_A → S be the blow-up morphism as above. Let us further assume that A is a smooth point of S. By the above description, the inverse image of A in _A is a smooth curve E_Aℙ¹ which sits in ℙ^n-1 as the locus of all directions which are tangent to S. Now, if L is a line in S which contains A then L -{A} is collapsed to a point B E_A under p_A. In general, there is a unique such line (in fact Q is essentially the only case where this is not the case). Thus, the elementary transformation from S to T with centre A is obtained by replacing the line L_A which contains A with a point B which lies on a line E_A which takes the place of L_A in the ruling of T.

Let us temporarily specialise to the case when the base of the ruling is isomorphic to ℙ¹.

Let C_d denote the rational normal curve of degree d in ℙ^d. Fix an isomorphism f_d : ℙ¹ → C_d. The projective spaces ℙ^d and ℙ^e can be put as disjoint linear spaces in the projective space ℙ^d+e+1; let us denote these by L^d and M^e respectively. Each point A of ℙ^d+e+1 which is not contained in L^d ∩ M^e gives rise (uniquely) to two points B and C in these linear spaces such that A lies on the line joining B and C in ℙ^d+e+1. The linear span of M^e and A meets L^d in a unique point B; similarly for C. The intersection of the span of M^e and A with the span of L^d and A is the line joining B and C. In particular, we see that the locus of lines joining f_d(t) with f_e(t) as t varies over ℙ¹ gives a ruled surface S_d,e in ℙ^d+e-1. A general hyperplane meets each of these lines in one point. It follows that the intersection of a general hyperplane with S_d,e gives a rational normal curve of degree d + e in ℙ^d+e. Consider a hyperplane H that contains L^d. Its intersection with S_d,e already contains C_d. Let A be a point of H ∩ S_d,e \ C_d. Let L be the line in S_d,e that contains A. Since L meets H and A as well as the endpoint of L that lies in C_d, we see that L lies in H. Thus (from degree considerations) it follows that H ∩ S_d,e in general consists of C_d and e lines L₁, …, L_e from the ruling. Similarly, a general hyperplane containing M^e intersects S_d,e in C_e and d lines from the ruling on S_d,e. Now, e general lines in a projective space ℙⁿ will have a linear span of dimension 2e - 1 as long as n ≥ 2e - 1. Thus, if d > e, the span of any e lines in the ruling of S_d,e determines a linear subspace of dimension 2e - 1 in ℙ^d+e+1; in particular, there are many hyperplanes that contain such an e-tuple of lines. The residual intersection of such a hyperplane with S_d,e gives a curve of degree d. One can easily show that this is another rational normal curve of degree d which too spans a linear subspace of ℙ^d+e+1 which is disjoint from M^e. On the other hand we cannot take the linear span of d general lines in this situation since their span will be all of ℙ^d+e+1. Using this one can show that C_e is the curve of least degree in S_d,e. Similarly, one can show that the elementary transform of S_d,e from a point not on C_e results in S_d-1,e, whereas the elementary transform of S_d,e from a point on C_e results in S_d,e-1.

In order to explain the next statement we need to introduce the notion of self-intersection of a curve on a surface S. Let S ⊂ ℙⁿ be a surface and C a curve on S. Let F be a general homogeneous polynomial of large degree that vanishes on C and let V (F) denote the hypersurface in ℙⁿ defined by the vanishing of F. One can show that V (F) ∩S is of the form C + D for D an irreducible curve on S. We define the self-intersection (C.C) of C as deg(C)deg(F) - (C ⋅D); where (C ⋅D) denotes the intersection of C and D as defined earlier. As in the case of most such definitions the main work goes into proving that this number is independent of the choice of F; in fact it is also independent of the embedding of S in projective space. We note that if H = ℙ^n-1 ∩ S is the intersection of S with a hyperplane in ℙⁿ then (H.H) = deg(H) = deg(S).

Returning to the ruled surfaces S_e,d, let L be a line which is the ruling of S_e,d. A general hyperplane that contains L will meet all other lines in the ruling transversely at one point. It follows that the intersection of such a hyperplane with S is of the form C + L where C meets L in exactly one point. Thus (L.L) = 0. Now some easy calculations show that (C_e.C_e) = e - d in S_d,e. In particular, when d > e this is a negative number. This is not un-correlated with what we showed above—viz. the curve C_e does not “move” in this case.

Let us move on to more general ruled surfaces. Let S ⊂ ℙⁿ be a ruled surface. We wish to study curves H on S with the property that they meet each line in the ruling of S transversely; such curves are called “sections” of the ruling for obvious reasons. By a procedure similar to the one used to construct S_d,e, it is not difficult to construct surfaces which have sections H where (H.H) can become as small as one wants. In the interests of restricting one’s attention to “interesting” surfaces one can look at the case where (H.H) is bounded below. One such restriction that has proved very worthwhile is to require that (H.H) > 0 for every section H. Such ruled surfaces are called “stable”. A slight weakening of this is to allow equality as well; in that case the ruled surface is called “semi-stable”.

M. S. Narasimhan and C. S. Seshadri were able to prove a remarkable topological description of stable (and semi-stable) ruled surfaces. This description could be used to find a parametrisation of all such surfaces. The study of these parameter spaces (or moduli spaces) has been the subject of numerous papers by algebraic geometers at the TIFR such as S. Ramanan, A. Ramanathan, V. B. Mehta, N. Nitsure, Y. Holla and others.