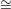We now study the problem of constructing parametric families of curves. To begin with let us restrict ourselves to the field ℂ of complex numbers.

As we have seen earlier, given a curve X of degree d in ℙⁿ, and a general linear subspace L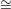ℙ^n-2 in ℙⁿ, the projection away from L gives a morphism f : X → ℙ¹ for which each fibre has d points except for 2d + 2g - 2 points where the fibre has d - 1 points; let S denote this finite set of points.

The morphism f : X \ f^-1(S) → ℙ¹ \ S is a covering space and so is determined by a homomorphism π₁(ℙ¹ \ S,p) → Perm(f^-1(p)), where p is some choice of base point and Perm(f^-1(p)) is the group of permutations of this finite set of d points. Since π₁(ℙ¹ \ S,p) is a free group with |S|- 1 generators, there are only finitely many such homomorphisms. Conversely, any homomorphism π₁(ℙ¹ \S,p) → Perm(T) gives a finite (not necessarily connected) cover whose fibre over p can be identified with T. In order that the cover is connected the image of this group homomorphism should act transitively on T. In order that the cover be similar to the description above it is necessary and sufficient that for each s in S, the elements of π₁(ℙ¹ \ S,p) corresponding to all sufficiently small loops around s, are mapped to transpositions in Perm(T). In summary, each such cover is determined by a map l : S → Perm(T) which lands in transpositions such that ∏ l_s is the identity and such that the image generates a transitive subgroup of Perm(T). (Exercise: Show that the homomorphism is surjective in this case).

From the above discussion we only need to note that the space parametrising such covers is itself a finite cover of the space parametrising (2d + 2g - 2)-tuples of points in ℙ¹. The latter is parametrised by the the quotient of an open subset of the space of all homogeneous polynomials of degree 2d + 2g - 2 in two variables under the action of the group of linear changes of co-ordinates in 2 variables. In other words, the space parametrising such covers is of dimension 2d + 2g - 5. The next question we need to ask is “how often” a given curve of genus g presents itself in this fashion.

For d sufficiently large, any effective divisor D of degree d on any curve X of genus g occurs as the hyperplane section of an embedding X ⊂ ℙ^d-g; in fact, by the Riemann-Roch theorem d > 2g is good enough. Think of this hyperplane as a point in (ℙ^d-g)^*. The locus of lines that contain this point can be identified with a complementary ℙ^d-g-1. For the general such D and the general line L containing it we obtain a morphism X → ℙ¹ as described above; these general conditions thus give us a (Zariski) open set in a space parametrising pairs (D,L). The space of effective divisors of degree d has dimension d and thus the space of such pairs has dimension 2d - g - 1. Thus, for a fixed curve X, the space of all maps f : X → ℙ¹ as described above is of dimension 2d - g - 2 (since we can “forget” the chosen fibre D).

Combining the above two paragraphs we obtain Riemann’s count for the moduli of curves of genus g; the difference (2d + 2g - 5) - (2d-g - 2) = 3g - 3 is the dimension of the space parametrising curves of genus g.

There are a number of difficulties with the above argument. Many of the arguments can be easily made more formal without losing the geometric flavour. However, the use of the complex topology and the existence theorem of Riemann (to ensure that every covering as described above comes from an algebraic curve) are much more difficult to sort out. In order to carry these arguments out over other fields one needs the techniques of “stable” morphisms between curves that were introduced and developed by Beauville, Harris, Mumford and others. Of late, the study of moduli spaces has received fresh impetus through its connections with “string theory” which is an attempt to provide a unified description of the fundamental interactions in physics. Theoretical physicists such as Ashoke Sen of HRI are interested in “string theory”.

Let us examine some consequences of the Riemann-Roch theorem and our earlier computations about the genus of plane curves. A smooth curve in ℙ² of degree d has genus (d - 1)(d - 2)∕2. Now most curves of degree d are smooth and the space of all homogeneous polynomials of degree d has dimension (d + 1)(d + 2)∕2; moreover, a polynomial and its transform under a linear change of co-ordinates clearly describe isomorphic curves. Thus the space of smooth plane curves of genus (d - 1)(d - 2)∕2 has dimension (d + 1)(d + 2)∕2 - 9; put differently, the space of smooth plane curves of genus g (which only exist when g is a triangular number) grows only linearly with g whereas the collection of all curves of genus g grows like 3g. Thus for all g sufficiently large (in fact for g > 3), the general curve of genus g does not occur as a plane curve even if g is a triangular number. (Exercise: Find a curve of genus 3 that does not occur as a plane curve).