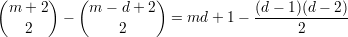
A smooth projective curve C over a field k is by definition a smooth irreducible projective variety of dimension 1 over k. To begin with let us think of C ⊂ ℙn for some unspecified n. Let us begin with a more detailed study of the arithmetic genus.
As an example consider a curve C ⊂ ℙ2 defined as the locus of vanishing of a homogeneous polynomial F(X,Y,Z) of degree d. It is clear that the homogeneous co-ordinate ring of C is R = k[X,Y,Z]∕(F) and so the dimension of Rm for all sufficiently large m is
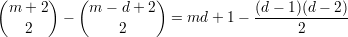
Thus we obtain that the arithmetic genus of a curve of degree d in ℙ2 is (d - 1)(d - 2)∕2. We notice that the dimension of Rm for small m does not obey this rule. In particular, the dimension of R1 is 3 as soon as F has no linear factor. Understanding this phenomenon will lead us to “special” linear series.
As mentioned in an earlier lecture, all morphisms from a curve C ⊂ ℙn can be seen as a composition of the Veronese embeddings and projections. From the definition given above it is clear that the Veronese embedding does not change the arithmetic genus. What about projection? By iteration, it is enough to examine what happens when we project from a single point on the curve. If we prove that the arithmetic genus is unchanged under an isomorphism induced by such a projection, then we will have proved that the arithmetic genus of a curve is an intrinsic invariant.
By a linear change of co-ordinates we can assume that point P we are projecting from has co-ordinates
(1 : 0 :  : 0). In that case the projection is seen ring-theoretically as taking the sub-ring S of R generated
by the variables X1,…,Xn. Now, we are also assuming that the curve in ℙn-1 is isomorphic to our original
curve C. If we examine what this means in terms of local co-ordinates on the curve C at the point P we see
that Sm consists of those F in Rm such that the first m Taylor coefficients of F∕X0m vanish at
the point. Now, we use the smooth-ness of the curve at the point which implies that there is
a linear polynomial (say X1) such that X1∕X0 is the local co-ordinate at the point P; then
X0kX1m-k are linearly independent elements of Rm that do not lie in Sm. It follows that for m
sufficiently large this subspace Sm has co-dimension exactly m in Rm. We thus see that the
dimension of Sm is m(d - 1) + 1 - g. It follows that the arithmetic genus is not changed by
projection.
: 0). In that case the projection is seen ring-theoretically as taking the sub-ring S of R generated
by the variables X1,…,Xn. Now, we are also assuming that the curve in ℙn-1 is isomorphic to our original
curve C. If we examine what this means in terms of local co-ordinates on the curve C at the point P we see
that Sm consists of those F in Rm such that the first m Taylor coefficients of F∕X0m vanish at
the point. Now, we use the smooth-ness of the curve at the point which implies that there is
a linear polynomial (say X1) such that X1∕X0 is the local co-ordinate at the point P; then
X0kX1m-k are linearly independent elements of Rm that do not lie in Sm. It follows that for m
sufficiently large this subspace Sm has co-dimension exactly m in Rm. We thus see that the
dimension of Sm is m(d - 1) + 1 - g. It follows that the arithmetic genus is not changed by
projection.
Consider a curve C ⊂ ℙn of degree d; it is natural to assume that C “spans” ℙn so that it does not lie in a linear subspace of ℙn. Such a curve is said to be non-degenerate curve in ℙn and we will henceforth restrict our attention to non-degenerate curves. A linear equation L defines a sub-variety of C consisting of at most d distinct points. Given any n points in ℙn, they lie in a ℙn-1. Hence, we must have d ≥ n for a non-degenerate curve. By applying this argument to the m-th Veronese embedding of the curve for sufficiently large m we see that md ≥ md - g or equivalently g ≥ 0.
Upon replacing the given embedding of C by a suitable Veronese twist we can assume that the dimension of Rm is dm + 1 - g for all m; note that d has been increased while ensuring this. Now, for any k ≤ d - g and any k points on the curve, consider all hyperplanes that contain these k points. This gives a linear system of hyperplanes of dimension at least d - k - g (it could be bigger if the k points are linearly dependent); moreover, the residual intersection (after leaving out the fixed k point locus) is of degree d-k. We generalise this statement below.
A divisor on a curve C is a finite formal expression of the form ∑ iniPi where Pi’s are points of C and ni’s are integers; in other words, the divisor group Div(C) is the free abelian group on points of C. A divisor is called effective if the ni’s are positive. A divisor A is said to contain a divisor B if the difference A - B is effective. The sum ∑ ini is called the degree of the divisor ∑ iniPi.
In an obvious way, each element F of the homogeneous co-ordinate ring R of C defines a divisor div(F). Since every point of C is an algebraic sub-variety, it is clear that every effective divisor is contained in a divisor of the type div(F) for some F in R. A divisor D is said to be linearly equivalent to zero if it is of the form div(F) - div(G) where F and G lie in some Rm (for the same m). Two divisors are said to be linearly equivalent if their difference is linearly equivalent to zero. In particular, it is clear that two divisors in a linear system as defined above are linearly equivalent.
Fix a divisor D = A-B where A and B are effective. Further, replace C by its Veronese embedding so that A is contained in div(L) for some linear L (i. e. L lies in R1), we can then write D as div(L) - B′ where B′ = B + div(L) - A is an effective divisor. The linear system of hyperplane divisors div(M) that contain B′ is gives a collection of effective divisors that are linearly equivalent to D; moreover, as seen above it has dimension at least deg(L) - deg(B′) - g. Thus we have proved Riemann’s inequality that the linear system of effective divisors linearly equivalent to a divisor D is of dimension at least deg(D) - g. In particular, given a divisor D of degree at least g there is an effective divisor that is linearly equivalent to it.
Now, if we fix an integer k, then the k-fold Veronese embedding of ℙn → ℙm (where m = 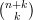 - 1) has
the property that the image of any k points of ℙn in ℙm gives a linearly independent set. (Hint: Use
Vandermonde determinant).
- 1) has
the property that the image of any k points of ℙn in ℙm gives a linearly independent set. (Hint: Use
Vandermonde determinant).
Let us replace C by a Veronese embedding chosen so that dim(Rm) = md + 1 - g and so that any g points on C are linearly independent. Let D be any effective divisor of degree d - g. Since dim(R1) = d + 1 - g, we see that D is contained in a hyperplane divisor div(L) for some L. Moreover, div(L) - D is a linearly independent set and so we see that the linear system of all divisors linearly equivalent to D is of dimension precisely deg(D) -g; such divisors could be called “general” divisors since we are interested in the special divisors for which such an inequality is strict. What we have just shown is that there is an upper bound on the degree of all special divisors. Let us note that if D is an effective divisor of degree less than g then it is automatically special; “some things become special just by existing!”
The Riemann-Roch theorem for curves implies the assertion that every effective special divisor is contained in a divisor linearly equivalent to a divisor KC whose degree is 2g - 2; this divisor (or strictly speaking its linear equivalence class) is called the canonical divisor of C. When g ≥ 2, there is a morphism C → ℙg-1 such that the inverse image of any hyperplane is a divisor linearly equivalent to KC. Special divisors on C can then be identified with effective divisors whose image lies in a hyperplane in C. In particular, any effective divisor D of degree at most g - 1 is clearly special. Given such a divisor D let ⟨D⟩ denote the linear span of D. In general, we will have dim⟨D⟩ = deg(D) - 1 but in some cases ⟨D⟩ will be smaller dimensional; in other words it will be even more special. The Riemann-Roch theorem for such divisors is the very elegant assertion that the dimension of the linear system |D| of effective divisors linearly equivalent to D is of dimension deg(D) - dim⟨D⟩- 1.
An open problem in the study of smooth projective curves is Green’s conjecture; this attracted the attention of S. Ramanan (a partial answer and new approach formed the basis of my Ph. D. thesis with him). He and V. Srinivas also gave a new approach to the problem. C. Voisin proved the conjecture for “most” curves a few years ago but since the conjecture deals with special divisors (and so special curves), the conjecture should still attract study from algebraic geometers. A concise statement of the conjecture is that it gives a precise relation between an explicit resolution of the co-ordinate ring of the canonical embedding of a curve and the special divisors (or as seen above linear dependent collections of points) on it.