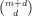 -1
given by
-1
given by
A correspondence between a pair of algebraic varieties X and Y can loosely be defined as a closed sub-variety Z of the product X × Y . One obvious example is the graph Γf of a morphism f : X → Y . However, note that there is a natural symmetry which interchanges correspondences between X and Y with those between Y and X; the notion of morphism does not have such a symmetry.
The problem we shall consider today is how one can construct interesting correspondences. So perhaps an easier question could be how does one construct interesting morphisms. Since we are only considering quasi-projective varieties, a morphism X → Y can be thought of as a morphism X → ℙn which happens to land inside the sub-variety Y ⊂ ℙn. We have thus simplified the question; we now only ask how one constructs morphisms from X to ℙn.
Since X is itself a sub-variety of ℙm for some m, we can try to construct morphisms from ℙm → ℙn and
go on from there. A fundamental example of such a morphism is the Veronese embedding ℙm → ℙ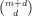 -1
given by
-1
given by
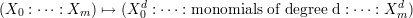
Another very important morphism is the projection ℙm \ ℙk → ℙm-k-1 given by
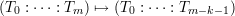
This morphism is cannot be extended along the sub-variety L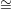 ℙk ⊂ ℙm given by the equations
T0 =
ℙk ⊂ ℙm given by the equations
T0 =  = Tm-k-1 = 0. In case our original variety X does not intersect L, then the morphism is defined
on X. With an eye on the notion of correspondences we can consider the closure in ℙm × ℙm-k-1
of the graph B of the above morphism. We note that B → ℙm is an isomorphism over the
open sub-variety ℙm \ L. The collection of all points in ℙm that are associated with a given
(x0 :
= Tm-k-1 = 0. In case our original variety X does not intersect L, then the morphism is defined
on X. With an eye on the notion of correspondences we can consider the closure in ℙm × ℙm-k-1
of the graph B of the above morphism. We note that B → ℙm is an isomorphism over the
open sub-variety ℙm \ L. The collection of all points in ℙm that are associated with a given
(x0 :  : xm-k-1) in ℙm-k-1 forms the linear subspace M(x0:
: xm-k-1) in ℙm-k-1 forms the linear subspace M(x0: :xm-k-1)
:xm-k-1)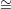 ℙk+1 given by the
equations xjTi = xiTj. It is clear that L ⊂ M(x0:
ℙk+1 given by the
equations xjTi = xiTj. It is clear that L ⊂ M(x0: :xm-k-1). In other words, we can think of B as
the space of all pairs (p,M) where M is a linear subspace of dimension k + 1 in ℙm such that
M contains L and the point p lies on M; when p is not in L, the linear span of p and L is
M.
:xm-k-1). In other words, we can think of B as
the space of all pairs (p,M) where M is a linear subspace of dimension k + 1 in ℙm such that
M contains L and the point p lies on M; when p is not in L, the linear span of p and L is
M.
More generally, we can perform a “blow-up” of any X such that no component of X is contained in L. Consider the restriction of the projection morphism to X \L. We obtain a space BX ⊂ X × ℙm-k-1 which is the closure of the graph of this morphism; this is called the blow-up of X along X ∩ L. The resulting correspondence is called a rational map on X.
The projection BX → X is an isomorphism over the open sub-variety X \ (X ∩L). However, it could be
an isomorphism on a bigger open sub-variety as well. In certain situations the first projection BX → X is an
isomorphism and then we obtain a morphism X → ℙm-k-1. It is an intriguing exercise to show that every
morphism X → Y from a quasi-projective variety to another can be obtained by these means. In
other words, given X ⊂ ℙm and Y ⊂ ℙn and a morphism f : X → Y , there is a d and a linear
subspace L in ℙ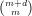 -1 such that the morphism f is obtained as the composition of the Veronese
embedding X → ℙ
-1 such that the morphism f is obtained as the composition of the Veronese
embedding X → ℙ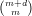 -1 with the projection from L, which is so chosen that B
X → X is an
isomorphism.
-1 with the projection from L, which is so chosen that B
X → X is an
isomorphism.
An important example is the case when X is a smooth curve; by this we mean a smooth irreducible projective variety of dimension 1. Let p be a point of X and consider the projection from p. One can see that BX is isomorphic to X; since there is “only one point missing” from X - p, the closure of this variety can only yield one more point! (Note the contrast between the algebraic context and the continuous context.) As an example, let us consider the curve in ℙ3 defined by the equations X2 + Y 2 = Z2 and aX2 + bY 2 = W2. Projecting this form a point on it gives a plane cubic curve in ℙ3. As an exercise you could try to write the equation of such a cubic.
Consider the variety Bℙm in ℙm × ℙm-k-1 which is obtained as the graph of the rational map (projection) ℙm \ ℙk → ℙm-k-1. It is also useful to think of it as a correspondence from ℙm-k-1 to ℙm. As seen above it can be thought of as the family of all k + 1 dimensional linear spaces in ℙm that contain the fixed ℙk from which we are projecting. This naturally leads us the the question of whether we can find the family of all ℙk’s in ℙm.
For example, let us consider the sub-variety I of ℙn × ℙn defined by the equation ∑
XiY i = 0, where
(X0 :  : Xn) and (Y 0 :
: Xn) and (Y 0 :  : Y n) are the projective co-ordinates on the two ℙn’s. For each point
(a0 :
: Y n) are the projective co-ordinates on the two ℙn’s. For each point
(a0 :  : an) of ℙn, the equation ∑
aiY i = 0 defines a linear sub-space of dimension n - 1 in ℙn.
Conversely, any such linear space is defined by such an equation. Hence, we see that I can be thought of the
variety parametrising such linear subspaces of dimension n - 1 — indeed, by symmetry this
is true whichever way we look at this correspondence; with respect to the first factor or the
second.
: an) of ℙn, the equation ∑
aiY i = 0 defines a linear sub-space of dimension n - 1 in ℙn.
Conversely, any such linear space is defined by such an equation. Hence, we see that I can be thought of the
variety parametrising such linear subspaces of dimension n - 1 — indeed, by symmetry this
is true whichever way we look at this correspondence; with respect to the first factor or the
second.
To take up a more asymmetric situation, let us consider the ℙ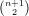 -1 whose projective co-ordinates we
think of as tuples (Xij) with the relations Xii = 0 and Xij + Xji = 0. We then define the sub-variety I of
ℙ
-1 whose projective co-ordinates we
think of as tuples (Xij) with the relations Xii = 0 and Xij + Xji = 0. We then define the sub-variety I of
ℙ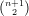 -1 × ℙn by the equations X
ijY k + XjkY i + XkiY j = 0 as i, j, k run over all possible values from 0 to
n.
-1 × ℙn by the equations X
ijY k + XjkY i + XkiY j = 0 as i, j, k run over all possible values from 0 to
n.
For each point (b0 :  : bn) of ℙn, the linear equations on the Xij given by substituting bi in place of Y i
give a linear subspace of ℙn; it is an exercise to show that this is a linear space of dimension n - 1. (Hint:
Try to show that if (xij) is a tuple satisfying these equations then xij = bicj - bjci for some ci). The
dimension of I is thus 2n- 1. One can similarly show that the linear space in ℙn defined by the equations
obtained on substituting Xij by any tuple aij (such that aii = 0 and aij + aji = 0) is of dimension 1 if it is
non-empty.
: bn) of ℙn, the linear equations on the Xij given by substituting bi in place of Y i
give a linear subspace of ℙn; it is an exercise to show that this is a linear space of dimension n - 1. (Hint:
Try to show that if (xij) is a tuple satisfying these equations then xij = bicj - bjci for some ci). The
dimension of I is thus 2n- 1. One can similarly show that the linear space in ℙn defined by the equations
obtained on substituting Xij by any tuple aij (such that aii = 0 and aij + aji = 0) is of dimension 1 if it is
non-empty.
It follows that the image of I in ℙ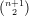 -1 is a variety of dimension 2n - 2; this is the Grassmannian
variety 𝔾(1,n). Plücker did the necessary elimination theory to write down the explicit equations for this
variety and so can you! One can generalise this approach to construct the Grassmannian variety 𝔾(k,n)
which parametrises ℙk’s in ℙn. The study of the geometry of the Grassmannian varieties (and other similar
varieties) has attracted numerous algebraic geometers including C. S. Seshadri, C. Musili, V. Lakshmibai,
A. Ramanathan, K. N. Raghavan and P. Sankaran.
-1 is a variety of dimension 2n - 2; this is the Grassmannian
variety 𝔾(1,n). Plücker did the necessary elimination theory to write down the explicit equations for this
variety and so can you! One can generalise this approach to construct the Grassmannian variety 𝔾(k,n)
which parametrises ℙk’s in ℙn. The study of the geometry of the Grassmannian varieties (and other similar
varieties) has attracted numerous algebraic geometers including C. S. Seshadri, C. Musili, V. Lakshmibai,
A. Ramanathan, K. N. Raghavan and P. Sankaran.
More generally, suppose one is trying to parametrise all sub-varieties of “type” X in projective space ℙn.
If the homogeneous co-ordinate ring of X is RX, one can say that Y has the same type as X if
the graded components satisfy dim(RY )m = dim(RX)m for all sufficiently large m. One can
find a degree d so that X is defined by equations of degree d. Consider the d-tuple Veronese
embedding of ℙn in ℙ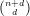 -1; denote the image by P
d. The sub-variety X in Pd is defined by linear
equations and is thus given by the intersection of Pd with a suitable linear space ℙk in the
ambient projective space. It is natural to expect (though it requires some effort to prove) that
other sub-varieties in ℙn of the same type as X are also obtained by intersecting Pd with linear
subspaces of the same dimension; in other words, every Y with the property given above is also
defined by same number of equations of degree d. However, it is unlikely (give an example!)
that all linear spaces of dimension k will intersect Pd in a variety of type X. The condition
that fixes the type will be a closed condition in the sense that there is a closed sub-variety of
𝔾(k,
-1; denote the image by P
d. The sub-variety X in Pd is defined by linear
equations and is thus given by the intersection of Pd with a suitable linear space ℙk in the
ambient projective space. It is natural to expect (though it requires some effort to prove) that
other sub-varieties in ℙn of the same type as X are also obtained by intersecting Pd with linear
subspaces of the same dimension; in other words, every Y with the property given above is also
defined by same number of equations of degree d. However, it is unlikely (give an example!)
that all linear spaces of dimension k will intersect Pd in a variety of type X. The condition
that fixes the type will be a closed condition in the sense that there is a closed sub-variety of
𝔾(k,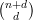 - 1) for which the type will be preserved. This variety parametrises sub-varieties in Pd
- 1) for which the type will be preserved. This variety parametrises sub-varieties in Pd ℙn
of the same type as X and is called the Hilbert scheme of subvarieties of type X in ℙn. One
can similarly construct Hilbert schemes of sub-varieties of a general projective variety Y . The
natural incidence between the Hilbert scheme and Y gives an example of a very interesting
correspondence.
ℙn
of the same type as X and is called the Hilbert scheme of subvarieties of type X in ℙn. One
can similarly construct Hilbert schemes of sub-varieties of a general projective variety Y . The
natural incidence between the Hilbert scheme and Y gives an example of a very interesting
correspondence.
To conclude this discussion let us take a simple example of the Hilbert scheme—the space of conics in ℙ2. Consider the sub-variety of ℙ2 × ℙ5 given by the equation
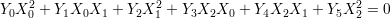
This exhibits ℙ5 as the space of conics in ℙ2.