


Next: 9.5 Frobenius Endomorphism
Up: 9 Hyperelliptic Cryptosystems
Previous: 9.3 Divisors
Let Q be any closed point in
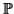 1 that is different from the
point
1 that is different from the
point 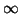 at infinity. As we saw above Q is given as a closed
subscheme of
at infinity. As we saw above Q is given as a closed
subscheme of
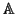 1 =
1 = 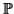 1 -
1 - 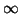 as the vanishing locus of an
irreducible polynomial f (x). If k = deg(f ) then consider the
f-fold Veronese embedding of
as the vanishing locus of an
irreducible polynomial f (x). If k = deg(f ) then consider the
f-fold Veronese embedding of
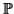 1 in
1 in
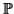 k. We see that Q is
precisely the intersection of the image of
k. We see that Q is
precisely the intersection of the image of
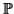 1 with the
hyperplane
V(a0X0 + ... + akXk) (if
f (x) = a0 + ... + akXk).
Moreover, V(X0) intersects the image of
1 with the
hyperplane
V(a0X0 + ... + akXk) (if
f (x) = a0 + ... + akXk).
Moreover, V(X0) intersects the image of
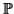 1 in a k-tuple
thickening of
1 in a k-tuple
thickening of 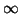 . From earlier remarks on the K-group we see
that
(Q) = k(
. From earlier remarks on the K-group we see
that
(Q) = k(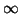 ) in
K(
) in
K(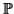 1).
1).
Now the morphism
T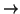
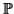 1 is flat and so we get a group
homomorphism
K(
1 is flat and so we get a group
homomorphism
K(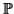 1)
1)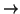 K(T). In particular, in the various cases
enumerated above, for closed points P in T that lie over closed
points Q in
K(T). In particular, in the various cases
enumerated above, for closed points P in T that lie over closed
points Q in
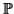 1 we have:
1 we have:
- The image of the element (
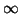 ) under this homomorphism is
2(
) under this homomorphism is
2(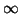 ).
).
- If Q is the closed point corresponding to an irreducible
factor of
a(x)2 - 4b(x), then the image of (Q) is 2(P).
- If f (x) is an irreducible polynomial so that
y2 + a(x)y + b(x)
is irreducible modulo f (x), then the image of (Q) is (P).
- If f (x) is an irreducible polynomial so that
y2 + a(x)y + b(x)
has distinct roots g(x) and h(x) modulo f (x), then there are
two closed points P and P' that lie over Q and the image of
(Q) is (P) + (P').
From the relation
(Q) = deg(Q)(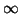 ) we obtain relations in each
case as follows. In case (2) we see that
deg(P) = deg(Q) so that
(Q) - deg(Q)(
) we obtain relations in each
case as follows. In case (2) we see that
deg(P) = deg(Q) so that
(Q) - deg(Q)(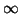 ) has the image
2[P] = 2(P) - 2 deg(P)(
) has the image
2[P] = 2(P) - 2 deg(P)(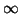 ); thus
[P] is a two torsion point in this case.
In case (3), we have
deg(P) = 2 deg(Q) and so that
(Q) - deg(Q)(
); thus
[P] is a two torsion point in this case.
In case (3), we have
deg(P) = 2 deg(Q) and so that
(Q) - deg(Q)(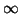 ) has image
[P] = (P) - deg(P)(
) has image
[P] = (P) - deg(P)(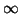 ); thus [P]
is 0 in this case. In case (4)
deg(P) = deg(P') = deg(Q) and the
image of
(Q) - deg(Q)(
); thus [P]
is 0 in this case. In case (4)
deg(P) = deg(P') = deg(Q) and the
image of
(Q) - deg(Q)(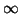 ) is [P] + [P'] which gives us the
identity
[P] + [P'] = 0.
) is [P] + [P'] which gives us the
identity
[P] + [P'] = 0.
Thus, elements of
Pic0(T) can be written in the form
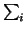 ni[Pi] +
ni[Pi] + 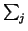 [Pj] where the former [Pi] are all of type (4)
and the latter [Pj] are of type (2). As we saw above, Hensel's
lemma allows us to lift the solution y = g(x) of the equation
y2 + a(x)y + b(x) modulo f (x) in case (4) to a solution y = gk(x)
modulo f (x)k for any k. Combining this with the Chinese remainder
theorem, we see that divisors are characterised as solutions y = g(x)
of
y2 + a(x)y + b(x) modulo f (x), where f (x) is not necessarily
irreducible. Conversely, given such a solution, let
Z = V(y - g(x), f (x))
and we have the divisor
(Z) - deg(f )(
[Pj] where the former [Pi] are all of type (4)
and the latter [Pj] are of type (2). As we saw above, Hensel's
lemma allows us to lift the solution y = g(x) of the equation
y2 + a(x)y + b(x) modulo f (x) in case (4) to a solution y = gk(x)
modulo f (x)k for any k. Combining this with the Chinese remainder
theorem, we see that divisors are characterised as solutions y = g(x)
of
y2 + a(x)y + b(x) modulo f (x), where f (x) is not necessarily
irreducible. Conversely, given such a solution, let
Z = V(y - g(x), f (x))
and we have the divisor
(Z) - deg(f )( ) in
Pic0(T).
) in
Pic0(T).
To summarise, each divisor class in
Pic0(T) is represented by a
pair of polynomials
(f (x), g(x)), where g(x) has degree less than
that of f (x) and
g(x)2 + a(x)g(x) + b(x) is divisible by f (x); as
we shall see below this representation is not unique. We can
further assume that any irreducible factor of f (x) that divides
a2(x) - 4b(x) divides f (x) at most once. Moreover, it is clear that
the inverse of this class in
Pic0(T) is represented by
(f (x), g1(x)), where g1(x) is the reduction modulo f (x) of
a(x) - g(x).
If
(f1(x), g1(x)) and
(f2(x), g2(x)) are two such pairs, then we
can form their sum in
Pic0(T) as follows.
- Assume that f1(x) and f2(x) are co-prime.
We find h1(x) and h2(x) so that
h1f1 + h2f2 = 1. Let g(x)
be the reduction of
h1f1g2 + h2f2g1 modulo f1f2. We see
that g(x) reduces to g1(x) modulo f1 and to g2(x) modulo
f2. Hence, by the Chinese Remainder Theorem it follows that
g(x)2 + a(x)g(x) + b(x) is divisible by
f (x) = f1(x)f2(x). Thus the
sum is
(f (x), g(x)).
- Now suppose that h(x) is a common factor of f1(x) and
f2(x). We further write
h(x) = h1(x)h2(x) where h1(x) is the
common factor of h(x) with
a2(x) - 4b(x). Since the corresponding
elements [P] (in case (2) as above) are of order 2 it follows that
this factor disappears when the sum is taken in
Pic0(T). In
other words, let f'1(x) and f'2(x) be the quotients of
f1(x) and f2(x) by h1(x) respectively, and let g'1(x)
and g'2(x) be the reductions of g1(x) by f1(x) and g2(x)
by f2(x) respectively. The sum of the pairs
(f'1(x), g'1(x))
and
(f'2(x), g'2(x)) is the same as the sum we want to compute.
- Assume that the common factor h(x) of f1(x) and f2(x)
is co-prime to
a2(x) - 4b(x). Let h1 be the highest common
factor of h with g1 + g2 - a and let h1 = h/h2. Now, both g1
and g2 a solutions of
y2 + a(x)y + b(x) = 0 modulo h1(x) and their
sum is a(x). It follows that these are complementary solutions as
in case (4) above. Thus these cancel out when the sum is taken in
Pic0(T). As in the previous case, we can replace the pairs
(f1, g1) and (f2, g2) by another pair with the same sum, with
the property that the f1, f2 and g1 + g2 - a have no common
factor.
- Assume that the common factor h(x) of f1(x) and f2(x) is
co-prime to
a2(x) - 4b(x) and to
g1(x) + g2(x) - a(x). Now, both
g1 and g2 are solutions of
y2 + a(x)y + b(x) = 0 modulo h(x)
and they are not complementary modulo any factor of h(x). By the
uniqueness part of Hensel's lemma it follows that g1(x) and
g2(x) is have the same reduction m(x) modulo h(x). Another
application of Hensel's lemma allows us to lift m(x) to a solution
mk(x) of the above equation modulo h(x)k, for every power k.
Now, we can write
f1(x) = n1(x)f'1(x) where f'1(x) has no
factor in common with h(x), moreover n1(x) is the greatest
common factor of f1(x) with
h(x)k1 for a suitable power
k1; similarly
f2(x) = n2(x)f'2(x). Let k be such that
h(x)k is divisible by
n1(x)n2(x). By using the Chinese
Remainder theorem as before, we can find g'(x) which lifts the
solutions mk(x) modulo h(x)k, g1(x) modulo f'1(x) and
g2(x) modulo f'2(x) to a solution modulo
h(x)kf'1(x)f'2(x). Reducing this solution modulo
f1f2 = n1n2f'1f'2, we obtain the required pair
(f (x), g(x)).
Finally we need to ``reduce'' divisors to a bounded collection. For
this we use our original description of the hyperelliptic curve T as
a closed subscheme of the cone Sd in
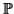 d + 1. We have
noted earlier that if L is any
d + 1. We have
noted earlier that if L is any
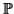 d sitting linearly in
d sitting linearly in
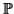 d + 1, then we have an exact sequence
d + 1, then we have an exact sequence
Now the restriction of
(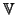 1×L)
1×L)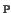 d + 1 to T is
(
d + 1 to T is
(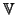 1×D)T where D is the divisor on T given by the
intersection of L and T. As remarked earlier, this shows that the
class in K0(T) of (L
1×D)T where D is the divisor on T given by the
intersection of L and T. As remarked earlier, this shows that the
class in K0(T) of (L 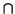 T) is independent of L. One such L
is V(X0) which intersects T in
2d (
T) is independent of L. One such L
is V(X0) which intersects T in
2d (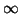 ). Thus, we note
that if
(L
). Thus, we note
that if
(L 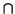 T) =
T) = 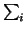 ni(Pi) then
ni(Pi) then
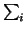 ni[Pi] = 0 in
Pic0(T).
ni[Pi] = 0 in
Pic0(T).
Now, any collection of d + 1 points in
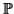 d + 1 lie on an L
which contains them. More generally, on can show the same for a
divisor of degree d + 1 on T. Now any L intersects T in a
divisor of degree 2d. In particular, given any divisor D of degree
d, we can find an L that contains
D + (
d + 1 lie on an L
which contains them. More generally, on can show the same for a
divisor of degree d + 1 on T. Now any L intersects T in a
divisor of degree 2d. In particular, given any divisor D of degree
d, we can find an L that contains
D + (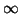 ), so that L
intersects T in
D + (
), so that L
intersects T in
D + (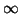 ) + E where E has degree d - 1. Thus,
we see that [D] + [E] = 0 in
Pic0(T). The inverse of [D] for a
divisor D of degree d is thus represented by [E] where E has
degree d - 1. This is the basic geometric idea behind the reduction of
divisors. The algebraic steps for this reduction are described below.
) + E where E has degree d - 1. Thus,
we see that [D] + [E] = 0 in
Pic0(T). The inverse of [D] for a
divisor D of degree d is thus represented by [E] where E has
degree d - 1. This is the basic geometric idea behind the reduction of
divisors. The algebraic steps for this reduction are described below.
As we saw above, elements of
Pic0(T) are represented by pairs
(f (x), g(x)), where g(x) has degree less than the degree of f (x)
and
h(x) = g(x)2 + a(x)g(x) + b(x) is divisible by f (x). Moreover, we can
also assume that f (x) is divisible at most once by any irreducible
factor that it has in common with
a(x)2 - 4b(x). Now if f (x) has
degree d + k, then h(x) has degree at most the
maximum of
{2(d + k - 1),(d - 1) + (d + k - 1), 2d - 1}. Thus writing
h(x) = f (x)f'(x) we see that f'(x) has degree at most the maximum of
{d + k - 2, d - 1}. Moreover, if g'(x) is the reduction of g(x)
modulo f'(x), then
(f'(x), g'(x)) is another pair representing an
element of
Pic0(T). Now, let
g(x) = 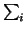 aixi have degree at
most d and put
G(X) =
aixi have degree at
most d and put
G(X) = 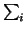 aiXi. Then
(f (x)f'(x), g(x))
represents the divisor L
aiXi. Then
(f (x)f'(x), g(x))
represents the divisor L 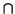 T where
L = V(Y - G(X)), thus we see that
(f'(x), g'(x)) represents the inverse of the element of
Pic0(T)
that is represented by
(f (x), g(x)) in this case. This argument can
be generalised to the case g has degree more than d as well (by
using the k-tuple Veronese embedding of
T where
L = V(Y - G(X)), thus we see that
(f'(x), g'(x)) represents the inverse of the element of
Pic0(T)
that is represented by
(f (x), g(x)) in this case. This argument can
be generalised to the case g has degree more than d as well (by
using the k-tuple Veronese embedding of
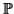 d + 1 and using
linear subspaces from there) to show the same result.
d + 1 and using
linear subspaces from there) to show the same result.
To summarise, we have two ways of representing the inverse of an
element of
Pic0(T) that is represented by the pair
(f (x), g(x)). One method is to let g1(x) be the reduction modulo
f (x) of a(x) - g(x) and take the pair
(f (x), g1(x)). The other
method is to take f'(x) to be the quotient of
g(x)2 + a(x)g(x) + b(x)
by f (x) and g'(x) to be the reduction of g(x) modulo
f (x). Combining these let f2(x) be the quotient by f (x) of
(a(x) - g(x))2 + a(x)(a(x) - g(x)) + b(x) = g(x)2 - a(x)g(x) + b(x)
and g2(x) be the reduction modulo f2(x) of a(x) - b(x). We see
that the pair
(f (x), g(x)) and the pair
(f2(X), g2(x)) represent
the same element in
Pic0(T). Moreover, if f (x) has degree d + k
for some k 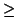 0, then f2(x) has strictly smaller degree. Thus
we have a method to reduce all pairs representing elements of
Pic0(T) to pairs
(f (x), g(x)) where f (x) has degree at most
d - 1.
0, then f2(x) has strictly smaller degree. Thus
we have a method to reduce all pairs representing elements of
Pic0(T) to pairs
(f (x), g(x)) where f (x) has degree at most
d - 1.



Next: 9.5 Frobenius Endomorphism
Up: 9 Hyperelliptic Cryptosystems
Previous: 9.3 Divisors
Kapil Hari Paranjape
2002-10-20
![]()
![]() 1 is flat and so we get a group
homomorphism
K(
1 is flat and so we get a group
homomorphism
K(![]() 1)
1)![]() K(T). In particular, in the various cases
enumerated above, for closed points P in T that lie over closed
points Q in
K(T). In particular, in the various cases
enumerated above, for closed points P in T that lie over closed
points Q in
![]() 1 we have:
1 we have:
![]() ni[Pi] +
ni[Pi] + ![]() [Pj] where the former [Pi] are all of type (4)
and the latter [Pj] are of type (2). As we saw above, Hensel's
lemma allows us to lift the solution y = g(x) of the equation
y2 + a(x)y + b(x) modulo f (x) in case (4) to a solution y = gk(x)
modulo f (x)k for any k. Combining this with the Chinese remainder
theorem, we see that divisors are characterised as solutions y = g(x)
of
y2 + a(x)y + b(x) modulo f (x), where f (x) is not necessarily
irreducible. Conversely, given such a solution, let
Z = V(y - g(x), f (x))
and we have the divisor
(Z) - deg(f )(
[Pj] where the former [Pi] are all of type (4)
and the latter [Pj] are of type (2). As we saw above, Hensel's
lemma allows us to lift the solution y = g(x) of the equation
y2 + a(x)y + b(x) modulo f (x) in case (4) to a solution y = gk(x)
modulo f (x)k for any k. Combining this with the Chinese remainder
theorem, we see that divisors are characterised as solutions y = g(x)
of
y2 + a(x)y + b(x) modulo f (x), where f (x) is not necessarily
irreducible. Conversely, given such a solution, let
Z = V(y - g(x), f (x))
and we have the divisor
(Z) - deg(f )(![]() ) in
Pic0(T).
) in
Pic0(T).
![]() d + 1. We have
noted earlier that if L is any
d + 1. We have
noted earlier that if L is any
![]() d sitting linearly in
d sitting linearly in
![]() d + 1, then we have an exact sequence
d + 1, then we have an exact sequence
![]() d + 1 lie on an L
which contains them. More generally, on can show the same for a
divisor of degree d + 1 on T. Now any L intersects T in a
divisor of degree 2d. In particular, given any divisor D of degree
d, we can find an L that contains
D + (
d + 1 lie on an L
which contains them. More generally, on can show the same for a
divisor of degree d + 1 on T. Now any L intersects T in a
divisor of degree 2d. In particular, given any divisor D of degree
d, we can find an L that contains
D + (![]() ), so that L
intersects T in
D + (
), so that L
intersects T in
D + (![]() ) + E where E has degree d - 1. Thus,
we see that [D] + [E] = 0 in
Pic0(T). The inverse of [D] for a
divisor D of degree d is thus represented by [E] where E has
degree d - 1. This is the basic geometric idea behind the reduction of
divisors. The algebraic steps for this reduction are described below.
) + E where E has degree d - 1. Thus,
we see that [D] + [E] = 0 in
Pic0(T). The inverse of [D] for a
divisor D of degree d is thus represented by [E] where E has
degree d - 1. This is the basic geometric idea behind the reduction of
divisors. The algebraic steps for this reduction are described below.
![]() aixi have degree at
most d and put
G(X) =
aixi have degree at
most d and put
G(X) = ![]() aiXi. Then
(f (x)f'(x), g(x))
represents the divisor L
aiXi. Then
(f (x)f'(x), g(x))
represents the divisor L ![]() T where
L = V(Y - G(X)), thus we see that
(f'(x), g'(x)) represents the inverse of the element of
Pic0(T)
that is represented by
(f (x), g(x)) in this case. This argument can
be generalised to the case g has degree more than d as well (by
using the k-tuple Veronese embedding of
T where
L = V(Y - G(X)), thus we see that
(f'(x), g'(x)) represents the inverse of the element of
Pic0(T)
that is represented by
(f (x), g(x)) in this case. This argument can
be generalised to the case g has degree more than d as well (by
using the k-tuple Veronese embedding of
![]() d + 1 and using
linear subspaces from there) to show the same result.
d + 1 and using
linear subspaces from there) to show the same result.