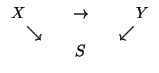
For any morphism T![]() S we can ``re-parametrise'' or perform base
change by associating
X×ST
S we can ``re-parametrise'' or perform base
change by associating
X×ST![]() T with X
T with X![]() S. One checks
that this gives a functor from the slash category /S to the slash
category /T.
S. One checks
that this gives a functor from the slash category /S to the slash
category /T.
For example, let N be any integer and consider the rings
![]() /N
/N![]() and
and
![]() [1/N]. The schemes over
Spec(
[1/N]. The schemes over
Spec(![]() /N
/N![]() ) are
the schemes ``modulo N''. The schemes over
Spec(
) are
the schemes ``modulo N''. The schemes over
Spec(![]() [1/N])
are schemes ``outside N''. In particular, we can take N = p a
prime to get schemes over
Spec(
[1/N])
are schemes ``outside N''. In particular, we can take N = p a
prime to get schemes over
Spec(![]() p) or schemes of characteristic
p. We occasionally see statements like ``the following is true
outside characteristic 2 and 3''; this can be interpreted as a
statement about schemes over
Spec(
p) or schemes of characteristic
p. We occasionally see statements like ``the following is true
outside characteristic 2 and 3''; this can be interpreted as a
statement about schemes over
Spec(![]() [1/6]).
[1/6]).
For many algebraic object that can be defined diagram-theoretically,
there are associated types of objects in the category /S. For
example we can define a group as a set G with maps
![]() : G×G
: G×G![]() G for multiplication,
G for multiplication,
![]() : G
: G![]() G for inverse and e : 1
G for inverse and e : 1![]() G which
maps the singleton set to the identity element of G. These satisfy
various commutative diagrams which ensure that multiplication is
associative, the product of an element and its inverse is identity and
the identity multiplied with anything is identity.
G which
maps the singleton set to the identity element of G. These satisfy
various commutative diagrams which ensure that multiplication is
associative, the product of an element and its inverse is identity and
the identity multiplied with anything is identity.
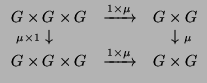
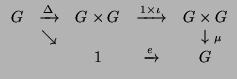
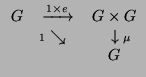
Thus we can define a group scheme over S as a morphism G![]() S with
morphisms in /S;
S with
morphisms in /S;
![]() : G×SG
: G×SG![]() G and
G and
![]() : G
: G![]() G and
e : S
G and
e : S![]() G which satisfy the same commutative diagrams. One example is
the scheme
G which satisfy the same commutative diagrams. One example is
the scheme
![]() m = Spec(
m = Spec(![]() [X, Y]/(XY - 1)) which is called the
multiplicative group of units since it associates to every finite ring
A the group of units in A.
[X, Y]/(XY - 1)) which is called the
multiplicative group of units since it associates to every finite ring
A the group of units in A.
Similarly a ring R is a set with maps
![]() : R×R
: R×R![]() R for
multiplication,
R for
multiplication,
![]() : R×R
: R×R![]() R for addition, - : R
R for addition, - : R![]() R for
negation, 0 : 1
R for
negation, 0 : 1![]() R for the zero element and 1 : 1
R for the zero element and 1 : 1![]() R for the
multiplicative identity. The various laws of associativity,
distributivity, commutativity (of addition) and additive and
multiplicative identity can again be formulated in terms of commutative
diagrams. We can use such diagrams to define the notion of a
ring scheme. One important example is that of
R for the
multiplicative identity. The various laws of associativity,
distributivity, commutativity (of addition) and additive and
multiplicative identity can again be formulated in terms of commutative
diagrams. We can use such diagrams to define the notion of a
ring scheme. One important example is that of
![]() a = Spec(
a = Spec(![]() [X])
called the additive group or the structure ring, since it associates
to each finite ring A the ring A itself with its natural
structure.
[X])
called the additive group or the structure ring, since it associates
to each finite ring A the ring A itself with its natural
structure.
We can similarly define the notion of group scheme actions on a scheme
and modules schemes over a ring scheme. One important example is that
of vector space schemes, which are group schemes that are also modules
over the ring scheme
![]() a. These are so called because, if V
a. These are so called because, if V![]() S is a vector space scheme over S and k is a finite field, then
the collection of all elements of V(k) that map to a fixed element
in S(k) acquire the natural structure of a vector space over k. We
can form a natural vector space scheme out of
S is a vector space scheme over S and k is a finite field, then
the collection of all elements of V(k) that map to a fixed element
in S(k) acquire the natural structure of a vector space over k. We
can form a natural vector space scheme out of
![]() q; we denote this
scheme by
q; we denote this
scheme by
![]() q. Clearly,
q. Clearly,
![]() q×S
q×S![]() S is a vector space
scheme over S for any S. Another example of a vector space scheme
the scheme TS considered above. This is called the (Zariski) Tangent scheme of S.
S is a vector space
scheme over S for any S. Another example of a vector space scheme
the scheme TS considered above. This is called the (Zariski) Tangent scheme of S.
Some other important examples of vector space schemes are as
follows. Let
H = V(0;X0, X1,..., Xp) be the complement of the point
(0 : ... : 0 : 1) in
![]() p + 1. The projection way from this point
gives a morphism
H
p + 1. The projection way from this point
gives a morphism
H![]()
![]() p. This is a vector space scheme with
``zero section'' given by
p. This is a vector space scheme with
``zero section'' given by
![]() p
p![]() H which maps
(a0 : ... : ap) to
(a0 : ... : ap : 0). For any i between 0 and
p we have sections
H which maps
(a0 : ... : ap) to
(a0 : ... : ap : 0). For any i between 0 and
p we have sections
![]() p
p![]() H given by sending
a0 : ... : aq) to
(a0 : ... : aq : ai). Considering the set
H given by sending
a0 : ... : aq) to
(a0 : ... : aq : ai). Considering the set
![]() p(A) as equivalence classes of surjective A-module
homomorphisms
Ap + 1
p(A) as equivalence classes of surjective A-module
homomorphisms
Ap + 1![]() A, it is clear that the kernel of this
homomorphism is independent of the chosen representative of the
equivalence class. This defines a sub-vector space scheme of
A, it is clear that the kernel of this
homomorphism is independent of the chosen representative of the
equivalence class. This defines a sub-vector space scheme of
![]() p + 1×
p + 1×![]() p
p![]()
![]() p. Another vector space scheme over
p. Another vector space scheme over
![]() p consists of the subscheme of
p consists of the subscheme of
![]() p + 1×
p + 1×![]() p which
is defined by
ViXj = VjXi; this vector space scheme is denoted
L.
p which
is defined by
ViXj = VjXi; this vector space scheme is denoted
L.
If V![]() S is a vector space scheme then for any morphism T
S is a vector space scheme then for any morphism T![]() S it
is clear that
V×ST
S it
is clear that
V×ST![]() T is one as well. In particular, vector
space schemes can be restricted to subschemes. The restriction
of the vector group scheme denoted H over
T is one as well. In particular, vector
space schemes can be restricted to subschemes. The restriction
of the vector group scheme denoted H over
![]()
![]() - 1 to the Veronese embedding of
- 1 to the Veronese embedding of
![]() p is
denoted
Hd
p is
denoted
Hd![]()
![]() p.
p.