


Next: 8.2 Functors of points
Up: 8 Algebraic Schemes for
Previous: 8 Algebraic Schemes for
We recall some basic facts about finite commutative rings with
identity (and 1 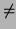 0). (The adventurous reader may like to explore
which parts of this entire section can be carried over to the
non-commutative case). The reader can prove these results from first
principles.
0). (The adventurous reader may like to explore
which parts of this entire section can be carried over to the
non-commutative case). The reader can prove these results from first
principles.
- In any finite ring there are finitely many ideals and in
particular there are finitely many maximal ideals. In other words
such a ring is ``semi-local''.
- Any prime ideal in a finite ring is maximal.
- (Analogue of Chinese Remainder Theorem). Any finite ring is a
product of finite local rings; i. e. finite rings which have
only one maximal ideal.
- In a finite local ring every element is either a unit or
nilpotent. Moreover, a finite local ring has pn elements for some
prime p and some integer n.
- The residue field of a finite local ring is the quotient
of the ring by its maximal ideal. This is a finite field.
- An element of a finite local ring is a unit if and only if its
image in the residue field is non-zero.



Next: 8.2 Functors of points
Up: 8 Algebraic Schemes for
Previous: 8 Algebraic Schemes for
Kapil Hari Paranjape
2002-10-20