To fix notation, let the quadratic order R be given as
![]() +
+ ![]() .
. ![]() , where
, where
![]() = (D +
= (D + ![]() )/2 with D = DR the
discriminant of the order R; then
)/2 with D = DR the
discriminant of the order R; then ![]() satisfies the equation
satisfies the equation
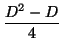 = 0
= 0
| a . |
= | p . a + q . (b + c |
|
| (b + c |
= | r . a + s . (b + c |
| a | = qc | and | 0 | = pa + qb | ||
| b + cD | = sc | and | -  |
= ra + sb |
Now, it is clear that the ideal
c-1I = ![]() . q +
. q + ![]() (- p +
(- p + ![]() )
is equivalent to I in the class group. Thus, we say the ideal is
primitive if the representative tuple (a, b, c) satisfies
c = 1. Clearly, we only need to look at primitive ideals for the
purpose of computing the class group; but there are more equivalence
relations.
)
is equivalent to I in the class group. Thus, we say the ideal is
primitive if the representative tuple (a, b, c) satisfies
c = 1. Clearly, we only need to look at primitive ideals for the
purpose of computing the class group; but there are more equivalence
relations.
We write a general element of I as
ax + (b + c![]() )y; its norm is a
multiple of
Nm(I) = ac. Thus,
)y; its norm is a
multiple of
Nm(I) = ac. Thus,
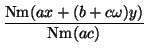 = qx2 + sxy - ry2
= qx2 + sxy - ry2
Now, if
I = ![]() . u1 +
. u1 + ![]() . u2, for some elements u1,
u2 in R, then the quadratic form
Qu1, u2(x, y) = Nm(xu1 + yu2)/Nm(I) is (in general) different
from QI(x, y). However, it is obtained from QI(x, y) by a
substitution
(x, y)
. u2, for some elements u1,
u2 in R, then the quadratic form
Qu1, u2(x, y) = Nm(xu1 + yu2)/Nm(I) is (in general) different
from QI(x, y). However, it is obtained from QI(x, y) by a
substitution
(x, y) ![]() (Ax + By, Cx + Dy) where
(Ax + By, Cx + Dy) where
![]()
![]()
![]() is an
integer matrix with integer inverse. One way to obtain a new basis is
to consider
I =
is an
integer matrix with integer inverse. One way to obtain a new basis is
to consider
I = ![]() . J for some ideal J in R and some
. J for some ideal J in R and some
![]() in K. Then, we write
J =
in K. Then, we write
J = ![]() . a' +
. a' + ![]() . (b' + c'
. (b' + c'![]() ) as before. Clearly
u1 = a'
) as before. Clearly
u1 = a'![]() and
u2 = (b' + c'
and
u2 = (b' + c'![]() )
)![]() is another basis of I.
is another basis of I.
Conversely, given a basis u1 and u2 of the ideal I, let d be
a denominator of u2/u1; i. e. d is a positive integer so that
du2/d1 lies in R. Consider the ideal
J = (d /u1) . I, we see
that
J = ![]() . d +
. d + ![]() . (du2/u1) and
J
. (du2/u1) and
J ![]()
![]() =
= ![]() . d.
Thus, as above we can find e and f so that 0
. d.
Thus, as above we can find e and f so that 0 ![]() e < d and
(du2/u1) = nd±(e + f
e < d and
(du2/u1) = nd±(e + f![]() ) for some integer n. Thus
J =
) for some integer n. Thus
J = ![]() . d +
. d + ![]() . (e + f
. (e + f![]() ). Putting
). Putting
![]() = u1/d we see that
u1 = d
= u1/d we see that
u1 = d![]() and
u2 = (nd±(e + f
and
u2 = (nd±(e + f![]() ))
))![]() ; in particular,
I =
; in particular,
I = ![]() . J. Moreover, we have
. J. Moreover, we have
Thus we have shown that QI(x, y) and QJ(x, y) are equivalent under an integer change of co-ordinates for the variables (x, y) if and only if the corresponding ideals are equivalent in the class group. The problem of finding representatives of ideal classes can be replaced by the problems of finding quadratic forms that represent equivalence classes.
We now separate the cases D < 0 and D > 0. In the first case, we
restrict our attention to quadratic forms
Q(x, y) = qx2 + sxy - ry2
(continuing the above notation) such that q > 0. Since
D = s2 + 4qr < 0,
we see that r < 0. In fact Q(x, y) > 0 for all
(x, y) ![]() (0, 0).
Pictorially, the region
Q(x, y)
(0, 0).
Pictorially, the region
Q(x, y) ![]() r is bounded by an ellipse. Thus,
among lattice points we can choose u1 to be an element where the
Q(u1) takes its minimum (non-zero) value. Now, we can complete
u1 to a basis by picking a suitable vector u2. The only possible
alternative choices for u2 are
nu1±u2 for some integer n.
Let u2 be so chosen that the value Q(u2) is minimum in this
collection. It is not too difficult to show that the expression for
Q in this basis is independent of the finitely many choices
available. (In fact for D| > 4 the choices of u1 and u2 are
unique upto sign). Now, in this basis we get
Q(x, y) = Ax2 + Bxy + Cy2
with A
r is bounded by an ellipse. Thus,
among lattice points we can choose u1 to be an element where the
Q(u1) takes its minimum (non-zero) value. Now, we can complete
u1 to a basis by picking a suitable vector u2. The only possible
alternative choices for u2 are
nu1±u2 for some integer n.
Let u2 be so chosen that the value Q(u2) is minimum in this
collection. It is not too difficult to show that the expression for
Q in this basis is independent of the finitely many choices
available. (In fact for D| > 4 the choices of u1 and u2 are
unique upto sign). Now, in this basis we get
Q(x, y) = Ax2 + Bxy + Cy2
with A ![]() C and | B|
C and | B| ![]() A. Moreover, if one of these is an
equality (which can only happen if | D|
A. Moreover, if one of these is an
equality (which can only happen if | D| ![]() 4), we have B
4), we have B ![]() 0 as
well. A quadratic form with negative discriminant is said to be reduced if it has this special form. Clearly, there are only
finitely many such forms for a given D; one for each equivalence
class of quadratic forms. Thus we have found representatives for the
class group.
0 as
well. A quadratic form with negative discriminant is said to be reduced if it has this special form. Clearly, there are only
finitely many such forms for a given D; one for each equivalence
class of quadratic forms. Thus we have found representatives for the
class group.
When D > 0, the quadratic forms are indefinite. The locus Q(x, y) = r represents a hyperbola. Now the value 0 is not attained at non-zero (x, y) (else D would have a square root in integers) and the values are all integers. Thus, the absolute value of Q attains a minimum at some point u1 on the lattice. But this u1 is far from unique (in fact there are infinitely many points where Q takes this value. One can show that upto a finite number of choices these are related by an integer change of co-ordinates. Now, as before, u1 can be completed to a basis by a choice of u2. The alternatives for this choice are nu1±u2 as earlier. Again, there are only finitely many of these with sign opposite to that of Q(u1) (since the term n2Q(u1) in the expansion of the quadratic form will dominate for n large). Among this finite set we choose u2 so that the absolute value of Q is minimum (again with only finitely many options for this choice). Thus, each equivalence class of quadratic forms has been represented upto a finite ambiguity. Moreover, one can bound the ambiguity depending on DR.