


Next: 3.1 Faster arithmetic
Up: Some Lectures on Number
Previous: 2.4 Extended GCD
Now that we have studied the basic arithmetic operations we can
perform computations in the ring
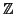 /N
/N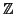 . The objects in this
ring are cosets of the form
a + N
. The objects in this
ring are cosets of the form
a + N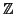 for integers b. By the process
of division we can write
a = d . N + r for r between 0 and N - 1.
Thus
b + N
for integers b. By the process
of division we can write
a = d . N + r for r between 0 and N - 1.
Thus
b + N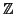 = r + N
= r + N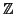 and so the objects of
and so the objects of
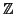 /N
/N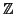 can be
identified with integers between 0 and N = 1. Thus one way to perform
arithmetic operations in this ring is to perform them with integers
and then, by division, reduce to this canonical form. However, this is
uses more space and time than required.
can be
identified with integers between 0 and N = 1. Thus one way to perform
arithmetic operations in this ring is to perform them with integers
and then, by division, reduce to this canonical form. However, this is
uses more space and time than required.
Subsections
Kapil Hari Paranjape
2002-10-20