


Next: 2.4 Extended GCD
Up: 2 Greatest common divisor
Previous: 2.2 Binary GCD algorithm
An alternate approach to speeding up Euclid's algorithm is due to
Lehmer. One notices that when a and b have the same size, the
integer part w of the quotient a/b is often single digit.
Secondly, the process underlying Euclid's algorithm is the
application of successive linear transformations (we will see this
also in the Extended GCD computations later)
Thus, we can repeatedly try to find the w as long as it is ``small''
and keep track of the operations involved by means of a matrix. When
we cannot proceed further, we apply this matrix to the original data,
and then try again. Occasionally, we many have to break out of a
``deadlock'' by performing a long division.
One way to check that w is small is to compare it with the quotient
a0/b0 of the leading digits of a and b, when a and b have
the same number of digits. More specifically if the integer part of
a0/(b0 + 1) and the integer part of
(a0 + 1)/b0 are equal, then
they are equal to w. The detailed algorithm is given below (we
assume a 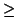 b).
b).
If b is a single digit then we apply Euclid's algorithm to get the
answer. Otherwise, we set x to be the leading digit (in base M) of
a and y to the the leading digit of b at the same place
(i. e. if
a = (a0...ap) then
b = (b0...bp) for the same p). We compute the invertible matrix
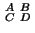
 ,
by an iteration of the following steps after initialising it as
the identity matrix.
,
by an iteration of the following steps after initialising it as
the identity matrix.
We compute the integer quotient w1 of
(x + A)/(y + C) and the integer
quotient w2 of
(x + B)/(y + D). We set w = w1 if w1 = w2 and
perform the matrix multiplication
We then replace our matrix by the resulting matrix. Similarly, we
replace x by y and y by x - wy. Then we iterate.
Lemma 4
In the above situation at most one of
y +
C and
y +
D is 0.
Moreover, we have the inequalities
| 0 |
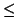 x + A x + A 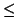 M M |
0 |
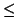 x + B < M x + B < M |
|
| 0 |
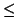 y + C < M y + C < M |
0 |
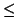 y + D y + D 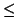 M M |
|
This ensures that all operations involved in this part of the
computation are digits. This procedure will exit when
w1 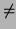 w2 or when one of y + C or y + D is 0.
w2 or when one of y + C or y + D is 0.
If the matrix computed has B = 0 then we need to perform a long
division operation using a and b (this case occurs only when the
first w1 and w2 and do not match). Otherwise, we replace a by
Aa + Bb and b by Ca + Db and go back to the start.
The advantage of this procedure is that long division is only
performed when absolutely essential; i. e. when the quotient w is
larger than M. One can show that this case occurs sufficiently
infrequently to account for the overhead of computing the matrix
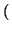
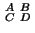
 .
.
Proof.
(of the lemma)
We only need to note that at any stage
x and
y are the result of
applying Euclid's algorithm to the original pair
x and
y.
Similarly,
x +
A and
y +
C at the same stage are the result of
applying Euclid's algorithm to the pair
x + 1 and
y; and
x +
B and
y +
D are associated to the pair
x and
y + 1. The lemma follows
from the consequence (of Euclid's algorithm) that these are all
decreasing and initially lie between 0 and
M.
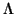



Next: 2.4 Extended GCD
Up: 2 Greatest common divisor
Previous: 2.2 Binary GCD algorithm
Kapil Hari Paranjape
2002-10-20
 .
. 
 .
. 
![]() b).
b).
![]()
![]()
![]() ,
by an iteration of the following steps after initialising it as
the identity matrix.
,
by an iteration of the following steps after initialising it as
the identity matrix.
 .
.  =
= 
![]()
![]()
![]() .
.